u003cstrongu003eCan compound interest make you rich?u003c/strongu003e

Unlike simple interest that carries a fixed interest, compounding on investments offer a higher return as they become bigger with time. This is because the interest is not fixed and is added to the investment amount in each period.u003cbr/u003eThe investment starts growing and earning a higher interest revenue when the interest is calculated on the enhanced amount every time. So the longer you hold the investment, the bigger it will grow.

Compound Interest

Compound Interest Definition

Compound interest is the interest charged on the sum of the principal amount and the total interest amassed on it so far. It plays a crucial role in generating higher rewards from an investment.

Banks typically opt for compound interests for a savings account, whereby interests earned on the bank balance are added back to it. Thus, the interest amount of each period keeps increasing after being calculated on a growing bank balance that is accumulating all the interests.

Compound interest is the interest computed on the sum of the initial investment amount and its accumulated interests. It is popularly understood as interest on interest.
The interest value is computed through the rate of return with an exponential growth factor; Compound Intererst Formula = P (1 + r/n) ᶺ nt.
To acquire the total interest receivable in future, subtract the principal sum (P) from the final amount receivable at the end of the tenure, i.e. (A).
Many investments provide compounding benefits like savings account, insurance products, stocks, mutual funds, bonds, CDs, REITs, treasury securities, and rental properties others.
People prefer their investments to benefit from compounding as it pays higher. Conversley, they desire their loans to accrue simple interests which is fixed throughout the tenure as it is calculated on the initial amount of principal.

Compound Interest Explained

You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Compound Interest (wallstreetmojo.com)

Compound interest is a method of interest calculation on loans or investments under which the values of accrued interestsAccrued Interests Accrued Interest is the unsettled interest amount which is either earned by the company or which is payable by the company within the same accounting period.read more vary throughout the tenure. The interest earned during each period is added back to the principal amount of a loan or investment. Thus, interest calculation of each term takes place on the inflated principal value, giving a different and enhanced return every single time.

It is in contrast to simple interests due to a difference in the method of computation. Simple interests offer a fixed interest as they are calculated on the initial investment amount for the entire term. Over the years, compound interest has become popular in common parlance, and it is said that the great Albert Einstein had reportedly called it the eighth wonder of the world.

Its recognition can be traced to the power of compoundingCompounding Compounding is a method of investing in which the income generated by an investment is reinvested, and the new principal amount is increased by the amount of income reinvested. Depending on the time period of deposit, interest is added to the principal amount.read more. Here, compounding reflects the number of times interest is charged or paid on the principal in a year. The compounding of interest occurs annually, semi-annually, quarterly, monthly and even daily. As such, the higher the frequency of compounding, the bigger the value of the principal.

Compound Interest Formula

The standard formula for compound interest (CI) can be modified for annual, quarterly, monthly, semi-annually or daily calculations. Let us go through this formula.

Compound Interest Formula = P (1 + r / n)^nt

Given below is an elaboration of the elements in the above equation and their relevance:

A denotes the final amount, which is the total amount an investor will get in future;
P represents the principal sum invested, i.e., the initial amount of investment;
r is the interest rate or rate of return at which the compounding takes place, say a 7% interest is written as 0.07 in the formula;
n signifies the number of the times the interest is compounded on the given amount. If compounding takes place semi-annually, n = 6, indicating interests paid twice in a year.
t is the period of investment in years, i.e., the number of years you want to keep your funds invested.

The amount of interest receivable in future is calculated as:

CI=A-P

We can calculate CI by deducting the initial investment from the future value of the invested amount.

Compounding Specifications

We had explained earlier that “n” refers to the compounding frequency in the formula above. Let us look at the formula again below –

A = P (1 + r / n)^nt

If compounding occurs annually, the n will be 1 to indicate once a year.
If compounding occurs quarterlyCompounding Occurs Quarterly The compounding quarterly formula depicts the total interest an investor can earn on investment or financial product if the interest is payable quarterly and reinvested in the scheme. It considers the principal amount, quarterly compounded rate of interest and the number of periods for computation.read more, the n will be 4 to indicate 4 times.
If compounding occurs daily, the n will be 365 to indicate daily accruing.

Compound Interest Calculation with Graph

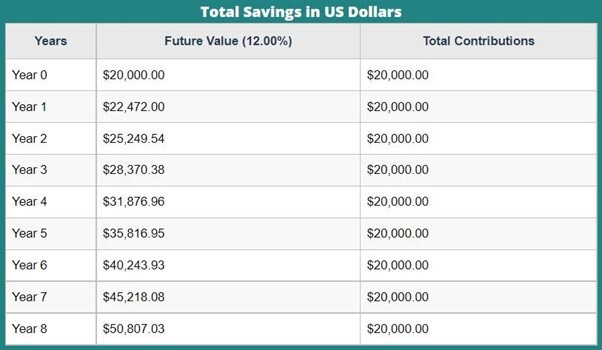
T invested $ 20,000 for 8 years tenure. Calculate the investment value after 8 years and the total interest receivable when the investment yields a return of 12 % compounded semi-annually.

Given:

P = $20000
r = 12%, i.e., 0.12
n = 2 (semi-annually, i.e., 12/6)
t = 8

A = P (1 + r/n) ᶺ nt

A = 20000 (1 + 0.12/2) ᶺ (2*8)
A = $ 50,807.03

CI = A – P

CI = 50807.03 – 20000
CI = $30807.03

Thus, T will receive a total amount of $50807.03 on completion of 8 years, while his overall returns would value $30807.03.

To comprehend the yearly appreciation of the principal amount, go through the table below of compounded values and a graph made from them.

How to Invest in Compound interest?

When a retirement scheme or savings account offers compound interest, the returns tend to be more rewarding than the earnings on simple interest. Moreover, if the frequency of compounding is more, the returns will multiply exponentially.

For example, in quarterly compounding, the interest will be paid four times a year. Consequently, it will reward higher earnings than annual compounding, where the interest will be paid only once a year. As such, the longer you hold the investment, the higher you’d make. As opposed to that, withdrawals will bring down the returns.

On the other hand, borrowers prefer their loans to attract simple interests instead of a climbing principal amount. Financial experts suggest borrowers pay off their debt obligations as early as possible if they carry compounding expenses to avoid burning a hole in their pockets.

Even if stocks or 401(K) accounts don’t actually earn such interests, they start giving an edge over other investments using the power of compounding. When stocks or bondsBonds Bonds refer to the debt instruments issued by governments or corporations to acquire investors’ funds for a certain period.read more held under a 401k account is reinvested into investment vehicles without being withdrawn, the accumulated lumpsum earns higher. Also, certain companies offer reinvestment of dividendsDividends When a company makes a profit at the end of the accounting year, it decides to distribute a portion of its earned profits to its stockholders, which is known as a dividend. Dividend ratio = Total Dividends / Net Income.read more under the real estate investment trusts (REITs).

As such, savings is linked closely with the power of compounding. Higher the saving, greater the earnings whenever investments allow compounding. When it comes to accruing compound interests, they are provided across bonds, certificate of deposits (CDs), credit cards, many bank accounts and loans.

Therefore, one must efficiently calculate compounding values before opting for any loans or investments. Since it could get quite cumbersome to work through a series of future values, several calculators are all over the web. In addition, many government platforms such as the SEC also offer these calculators with options to tweak for annual, monthly, quarterly or daily compoundingDaily Compounding Daily Compound Interest refers to the total interest amount, including the amount of interest earned on the initial principal & the amount of interest earned daily. It might be higher than Monthly or Quarterly Compound Interest due to the high compounding frequency. read more.

FAQs

What is a compound interest example?

There are many examples, with one being credit cards. Users of credit cards have to pay off the interest charges on the balance amount along with any previous period’s unpaid interest.

Can compound interest make you rich?

Unlike simple interest that carries a fixed interest, compounding on investments offer a higher return as they become bigger with time. This is because the interest is not fixed and is added to the investment amount in each period.
The investment starts growing and earning a higher interest revenue when the interest is calculated on the enhanced amount every time. So the longer you hold the investment, the bigger it will grow.

What is the Rule of 72?

Rule of 72 determines the number of years it will take for an investment to double. It applies to the investments providing annual compounding and the rate of which lies preferably between 6% to 10%. Here you have to divide the given interest rate (only the number) by 72. Say, an investment providing an 8% interest compounded annually will double its initial investment value in 9 years (72/8).

19th/20th September 2020	Saturday - Sunday	9 am IST to 5 pm IST
26th/27th September 2020	Saturday - Sunday	9 am IST to 5 pm IST

Compound Interest