Fisher Index

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Fisher-Price Index Definition

The Fisher-Price Index is a consumer price index used to measure the increase in prices of goods and services over time. It is calculated as the geometric mean of the Laspeyres Index and the Paasche Price Index.

Fisher-Price Index Definition

The Fisher-Price Index is a consumer price index utilized to calculate the increase in prices of goods and services over time.
It is calculated as the Laspeyres index and the Paasche Price Index geometric mean.
Fisher-Price Index is generally called the real index. It corrects for the Laspeyres Price Index's upward bias and the Paasche Price Index's downward bias by taking the average of the two weighted indices using the current and base year quantities as weight.
Though Fisher-Price Index is the better of the three indices, Laspeyres Price Index is more commonly used to calculate inflations.

Fisher Index Formula

Fisher-Price Index = (LPI*PPI)^0.5

where,

LPI = Laspeyres Price Index = ∑(Pn,t) * (Qn,0) * 100 / (Pn,0) * (Qn,0)

PPI = Paasche Price Index = ∑(Pn,t) * (Qn,t) * 100 / (Pn,0) * (Qn,0) ,

where

Pn,t is the price of the item at the n^th period
Pn,0 is the price of the item at the base period
Qn,t is the quantity of the item at the n^th period
Qi,0 is the quantity of the item at the base period

Examples of Fisher-Price Index

Below are the examples of a Fisher-Price Index.

Example #1

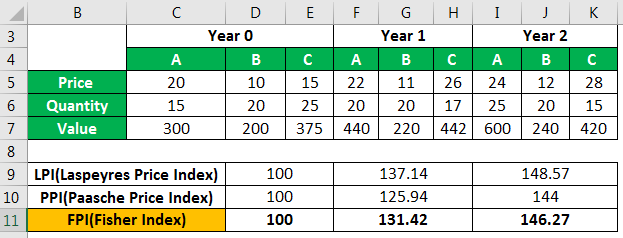
Let us find the Fisher-Price Index for three items whose price and quantity sold are given for three years. For example, for the current year designated as year 0, the prices in dollars and the quantity are provided as follows: -

	Year 0	Year 1	Year 2
	A	B	C	A	B	C	A	B	C
Price	20	10	15	22	11	26	24	12	28
Quantity	15	20	25	20	20	17	25	20	15
Value	300	200	375	440	220	442	600	240	420

First, we will calculate the Fisher-Price Index for Year 0 using Laspeyres Price Index and Paasche Price Index.

Laspeyres Price Index for Year 0 -

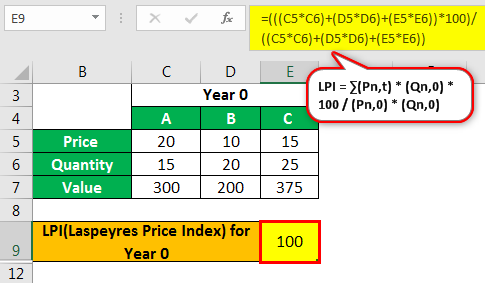
For Year 0 the Laspeyres Price Index (LPI) = (20*15+10*20+15*25)*100/ (20*15+10*20+15*25)
= 100

Paasche Price Index -

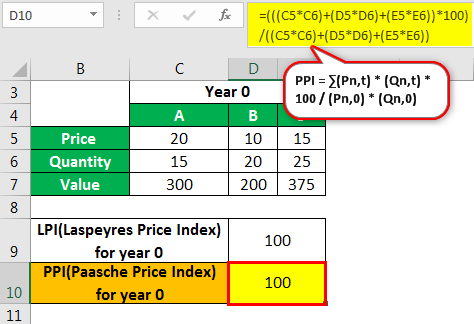
Paasche Price Index = (20*15+10*20+15*25)*100/ (20*15+10*20+15*25)
= 100

Fisher-Price Index for Year 0 -

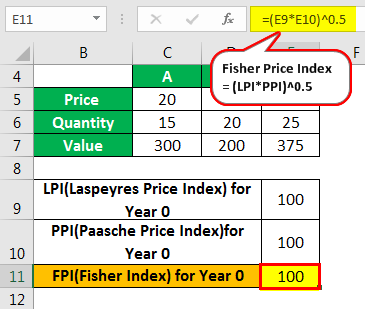
Fisher-Price Index(FPI) = (100*100)^0.5
= 100

Similarly, we find the indexes for Years 1 and 2 as given.

For Year 1

Laspeyres Price Index

LPI = (22*15+11*20+26*25)*100/ (20*15+10*20+15*25)
= 137.14

Paasche Price Index

PPI = (22*20+11*20+26*17)*100/ (20*15+10*20+15*25)
= 125.94

Fisher-Price Index (FPI)

FPI = (137.4*125.94)^0.5
= 131.42

For Year 2

Laspeyres Price Index

LPI = (24*15+12*20+8*25)*100/ (20*15+10*20+15*25)
= 148.57

Paasche Price Index

PPI = (24*12+12*20+28*15)*100/ (20*15+10*20+15*25)
= 144

Fisher-Price Index

FPI = (148.57*144)^0.5
= 146.27

We have given a tabular representation of the indexes in the following table.

Example #2

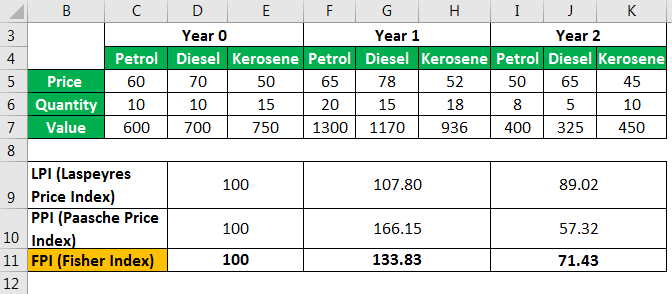
Let us consider three commonly used fuels: petrol, diesel, and kerosene. Now, calculate the price indices for three years.

The price in dollars and quantities in liters are shown in the following table: -

	Year 0	Year 1	Year 2
	Petrol	Diesel	Kerosene	Petrol	Diesel	Kerosene	Petrol	Diesel	Kerosene
Price	60	70	50	65	78	52	50	65	45
Quantity	10	10	15	20	15	18	8	5	10
Value	600	700	750	1300	1170	936	400	325	450

We can see that the price of fuels increased in Year 1 and decreased in Year 2. Did you notice that the quantities also show a similar trend, which is not surprising as we know that oil and gas exploration companies often reduce production when crude oil (the raw material) price falls?

The table showing the values of the indices, in this case, is given below and can be derived exactly in the same manner as shown in the above example.

Advantages of the FPI

Fisher-Price Index is often called the real index. It corrects for the upward bias of the Laspeyres Price Index and the downward bias of the Paasche Price Index by taking the geometric average of the two weighted indices. It uses both current year and base year quantities as weight.
Although it is not a frequently used index due to its structural complexity and the number of variables required, it has widespread use in academic circles and research.

Disadvantages of the FPI

The only limitation of the Fisher-Price Index is that it is a little more complex construct than the other two.
The quantities of the future years have to be forecasted, while in the Laspeyres Price Index, only the future prices have to be found.

Conclusion

Although the Fisher-Price Index is the better of the three indices, Laspeyres Price Index is more commonly used for inflation calculations. But if we can accurately forecast future quantities of an item, the Fisher-Price Index gives a more accurate measure.

Frequently Asked Questions (FAQs)

1. Why is Fisher-Price Index called the ideal index number?

The Fisher-Price Index is called the ideal index number because it overcomes the limitations of the other two commonly used index numbers, namely the Laspeyres Index and the Paasche Index.

2. Who proposed Fisher-Price Index?

The Fisher-Price Index was proposed by Irving Fisher and R. G. D. Allen independently in 1923.

3. What are the applications of the Fisher-Price Index?

The Fisher-Price Index has several applications, including:
Measuring inflation: The index can track the inflation rate by comparing the prices of a basket of goods and services over time.
Adjusting wages and salaries: The index can be used to adjust wages and salaries to reflect changes in the cost of living.
Deflating nominal values: The index can convert nominal values to real values by adjusting for inflation.
International trade: The index can be used to compare the cost of living between countries, which can help in international trade negotiations.