High Low Method Vs Regression Analysis

Difference Between High Low Method And Regression Analysis

The High Low Method and Regression Analysis in cost accounting help estimate the fixed and variable costs in a mixed-cost industry or firm. The main difference between the methods is that the high low method considers only two values – the highest and lowest activity costs, whereas the regression analysis considers the entire dataset.

While this difference is essential, primarily when outliers exist, each method will be appropriate depending on the data set.

• The high low method and regression analysis are cost estimation techniques used in accounting and budgeting.
• The high low method separates the fixed and variable costs by considering the values corresponding to the highest and lowest volume activities.
• The regression analysis method determines the relationship between a dependent variable and one or more independent variables, where the former changes with the latter.
• The dataset's accuracy and reliability are essential parameters in deciding which method to adopt. Based on the choice, the result varies.

Comparative Table

Let's look at the difference between the two in the following table:

Basis	High Low Method	Regression Analysis
Technique	This method considers the costs at the highest and lowest activity levels in the dataset.	The whole dataset of costs is analyzed to compare the dependence of a variable over one or more independent variables.
Dataset	A simple dataset is enough to apply the high low method. If the analyst needs complete data, this is the method to use.	If the dataset is reliable and complete, regression analysis can produce the best results for the analyst.
Advantages	The method is simple to use and easy to understand.	The method considers dataset outliers, too, thus making it more accurate.
Disadvantages	The outliers are overlooked by only considering the extreme cases, which might affect the results.	The method is complicated as it uses multiple variables and graphs to produce results.

What Is High Low Method?

The high low method is a technique used to segregate the fixed and variable costs associated with a product, equipment, or asset. This method is characterized by its minimal data requirements for differentiation, focusing on the respective costs at the highest and lowest activity levels for a comparative analysis. Let's explore the application of this method.

Calculation

• Step 1: Estimate the variable cost per unit.

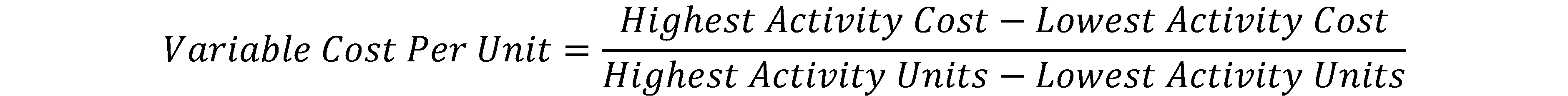
• Step 2: Determine the total fixed cost.

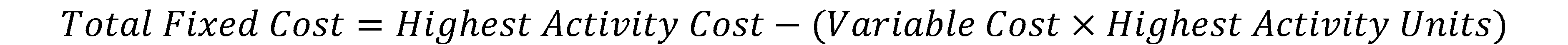
Alternatively,

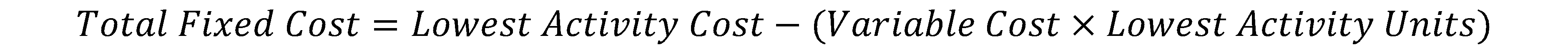
• Step 3: Find the high low cost.

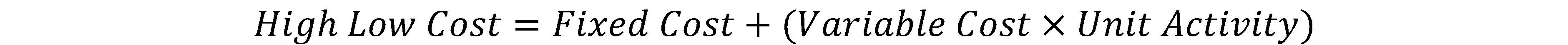
In summary, the high low method involves comparing the costs at the highest and lowest activity levels, considering both the cost and volume aspects. While the method is straightforward and requires minimal data, it is limited by its focus on only two extreme situations, and its applicability extends to the entire dataset's conclusion. Additionally, it does not account for the impact of inflation on costs.

Example

The data on total hours worked and the total cost is given. Find the fixed and variable costs.

Month	Total Cost	Quantity
July	$60,000	6500 units
August	$65,000	6000 units
September	$57,500	5500 units
October	$75,000	7000 units
November	$55,000	5750 units
December	$70,000	7500 units

Variable cost per unit = ($70,000 - $57,500) / (7500-5500) = $12,500 / 2000 = $6.25

Fixed cost = $70,000 - ($6.25 ⨉ 7500) = $70,000 - $46,875 = $23,125

High Low cost = $23,125 + ($6.25 ⨉ 7500) = $23,125 + $46,875 = $70,000

Thus, the case is satisfied.

What Is Regression Analysis?

Regression analysis is a statistical technique that helps establish the relationship among two or more variables. It measures the degree of change in the dependent variable while the independent variable(s) is/ are held constant. Regression analysis can be the most reliable cost estimation method, provided the data set is complete.

The regression analysis has three types – linear, non-linear, and multiple regression. In cost accounting, the first two methods are helpful.

Linear Regression

Linear regression analysis considers two variables, X and Y, where X is the independent variable, and Y is the dependent variable. This method helps determine the effect of X's change on Y. When plotted on a graph, these variables create a straight regression line described by the formula:

Y = a + bX + ε

Where,

• a is the intercept of the regression line, representing the value of Y when X is zero. In the context of cost accounting, it is often referred to as the fixed cost.
• b is the slope of the line, indicating the change in Y for a one-unit change in X. In cost accounting, this represents the variable cost per unit.
• ε is the residual error, accounting for unexplained variability in Y that is not captured by the linear relationship. It is important to note that the residual error is not always zero; rather, it represents the deviation of the actual values from the predicted values.

Multiple Regression

Multiple regression analysis helps determine the impact of two or more independent variables on a single dependent variable. This type of regression can also be plotted on a graph. It can be calculated as:

Y = a + bX₁ + cX₂ + dX₃ + … + e

Where,

• Y is the dependent variable
• X₁, X₂, X₃, … are the independent variables

Note: A scatter graph can help identify the dataset outliers while performing a regression analysis so that the result is accurate.

Example

The data on total hours worked and the total cost is given. Find the fixed and variable costs.

Month	Hours (x)	Cost (y)	X2	Y2	xy
July	1000	$60,000	1,000,000	3,600,000,000	60,000,000
August	950	$65,000	902,500	4,225,000,000	61,750,000
September	1025	$57,500	1,050,625	3,306,250,000	58,937,500
October	1000	$75,000	1,000,000	5,625,000,000	75,000,000
November	900	$55,000	810,000	3,025,000,000	49,500,000
December	1100	$70,000	1,210,000	4,900,000,000	77,000,000
Sum	5975	382,500	5,973,125	24,681,250,000	382,187,500

Using the least squares regression method, we can find the variable cost as the slope and the fixed cost as the intercept.

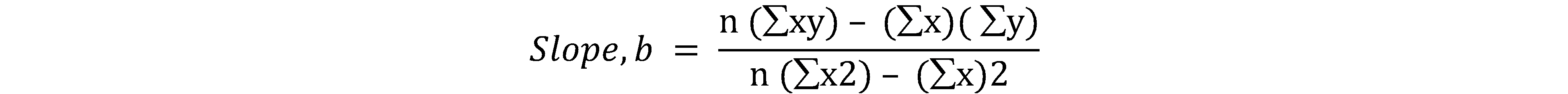
n = 6 (number of observations)

= 7,687,500 / 138,125 = 55.65

Variable cost per unit = $55.65

Using the linear regression formula,

Taking the first value of July,

Y = $60,000 = a + ($55.65 ⨉ 1000)

a = $60,000 - $55,650

Fixed cost = $4350

Similarities

Both the high low method and regression analysis share a common purpose – estimating fixed and variable costs in a mixed-cost industry. These methods play a crucial role for product managers and accountants in expense management. Beyond their shared objective, both approaches involve analyzing historical data to identify patterns and relationships between variables. This historical analysis aids in predicting future costs, enabling managers to implement effective control measures based on a more comprehensive understanding of cost structures.

Recommended Articles

This article has been a guide to High Low Method Vs Regression Analysis. Here, we explain the concepts through comparative table, similarities, and examples. You may also take a look at the useful articles below –

• Multinomial Logistic Regression
• Ordinal Regression
• Kernel Regression