Markowitz Model

The Markowitz model is a method of maximizing returns within a calculated risk. It is also called the Markowitz portfolio theory or modern portfolio theory. This model facilitates practical application; many new investors use this technique in capital markets.

The Markowitz model of selection mainly focuses on portfolio diversification. It separates stocks into high-risk and low-risk assets. The Harry Markowitz Model was introduced in 1952 through the journal of finance. Harry Markowitz won the Nobel prize for his contribution in 1990.

• The Markowitz model is an investing strategy. Amateur investors use it to maximize gross returns within a sustainable risk bracket.
• The Harry Markowitz Model was first published in the journal of finance in 1952. In 1990, Harry Markowitz won the Nobel Prize for his work on modern portfolio theory.
• The limitations of Markowitz model include overreliance on historical data, irrelevant assumptions, and the use of mean-variance instead of potential risks.
•  Markowitz's assumptions become irrelevant; this is especially the case with volatile markets.

The Markowitz model is an investment technique. It is used to create a portfolio that would yield maximized returns. In 1952, Harry Markowitz published his model in the Journal of Finance. Markowitz is an American economist. He is considered the creator of the modern portfolio theory. The theory is also known as the Markowitz Mean Variance Model.

The Markowitz model of portfolio suggests that the risks can be minimized through diversification. Simultaneously, the model assures maximization of overall portfolio returns. Investors are presented with two types of stocks—low-risk, low-return, and high-risk, high-return stocks. Risks are also divided into two—systematic risk and unsystematic risk. The Harry Markowitz model uses mathematical calculations to reduce risks; it builds an ideal portfolio.

Nonetheless, real-world investments cannot eliminate a certain level of risk. Thus, investors must possess some risk appetite. New investors especially benefit from this theory—the Markowitz model of portfolio popularized diversification. Not to mention the importance of understanding and avoiding systematic portfolio risks.

On the downside, the limitations of Markowitz model stem from its overreliance on assumptions. These flaws can make the conclusions irrelevant to prevailing market conditions.

Markowitz's assumptions are as follows:

• The model assumes that investors are rational and will always behave in a certain manner.
• The model assumes that there are only two different types of assets—low returns and high returns.
• Harry Markowitz argues that markets will always work in a certain direction and will always be efficient. But this is not always the case.
• Diversification is important. But the theory assumes diversification is the only way to minimize investment risks.
• The Markowitz model of portfolio assumes that every investor has unlimited access to information about market changes. In reality, investors often lack the time and expertise to gather relevant data.
• Markowitz assumes that all investors are risk-averse, but that is not universally true.
• The model mentions a bracket of bearable loss—but not all real-world investors can afford that.  

The Markowitz model diagram is as follows.

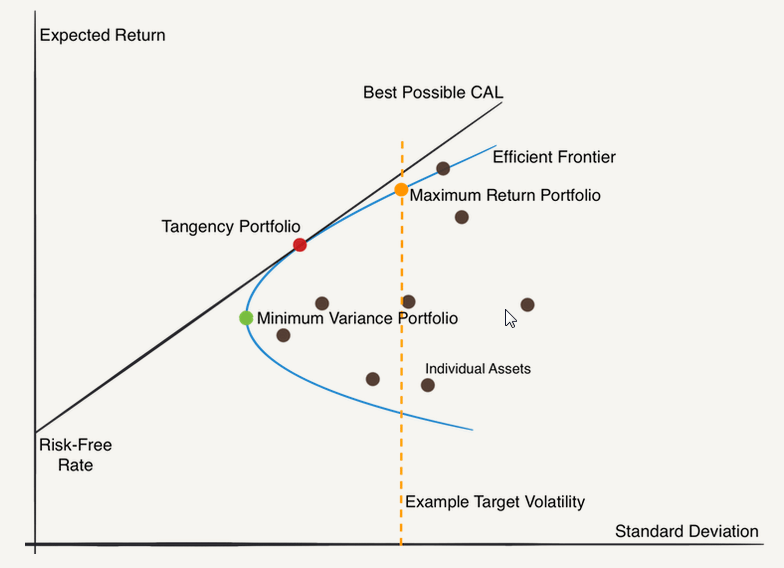
The Markowitz diagram depicts the standard deviation (risk) on the x-axis and expected returns on the y-axis. The diagram elucidates three portfolios:

1. Minimum variance portfolio
2. Tangency portfolio
3. Maximum return portfolio

The efficient frontier is a parabola depicting all three portfolios toward efficiency. The agency portfolio is also the optimal one—with the highest Sharpe ratio.

In contrast, the minimum variance portfolio is the green point in the diagram. It marks the change from convex to concave. Finally, the maximum return portfolio is the orange point—it has the highest volatility.

In the Markowitz diagram, portfolios on the efficient frontier are better than those under it. This is because the point where the linear Capital Market Line (CML) touches the y-axis is a risk-free asset.

The Markowitz formula is as follows:

R_P = I_RF + (R_M – I_RF)σ_P/σ_M

Here,

• R_P = Expected Portfolio Return
• R_M = Market Portfolio Return
• I_RF = Risk-free Rate of Interest
• σ_M = Market’s Standard Deviation
• σ_P = Standard Deviation of Portfolio

Let us now look at a Markowitz example to understand the theory better.

Let us assume that Charlie is an investor who possesses a small portfolio—only two stocks. He has invested $900,000 in stock A and $180,000 in stock B—a portfolio of $1080000. Charlie anticipates a 4% return on stock A and a 9% return on stock B.

To calculate the portfolio’s expected returns, we divide the current value of stock A by the total portfolio value and multiply it by its expected return:

• Portfolio expected return = $900,000/1080000 x 4%.

Now, we repeat the step for the second asset:

• Portfolio Expected Return = $180,000/1080000 x 9%.

So, for stock A (most invested), Charlie gets an expected return of 3%; for stock B (least invested), Charlie gets an expected return of 2%. The portfolio can expect a return of 5%.

To increase the expected portfolio return to 6.5%, Charlie needs to shift an appropriate amount of capital towards stock B (less invested).

A 50-50 allocation of capital will result in the following returns:

Portfolio Expected Return of 6.5%

• 50% x 4% = 2%

• Plus 50% x 9% = 4.5%

• Portfolio Expected Return = 2% + 4.5% = 6.5%

Let's assume Charlie divides the $1080000 portfolio into four equal assets. The first asset has a beta of 1, so its systematic risk exposure is identical to the market. The second asset has a beta of 1.6, as Charlie is willing to take a bit more risk. The third has a beta of 0.75—less exposure than the market; the fourth has an even lower beta of 0.5.

Multiplying the allocation of 25% with their respective beta values and adding the results give Charlie an overall portfolio beta value of 0.96. Since it is below 1, the portfolio is considered a systematic risk.

Let us consider another hypothetical; Charlie shifts 10% of the third and fourth assets with the lowest risk betas and 5% from the first division and invests in the second asset (highest-beta asset). Here the second asset, which started with a 25% allocation, will become 50% of the total portfolio's capital, the first amounts to 20%, and the third and fourth divisions account for 15% each.

• First division beta = 20% x 1 = 0.2

• Second division beta = 50% x 1.6 = 0.8

• Third division beta = 15% x 0.75 = 0.11

• Fourth division beta = 15% x 0.5 = 0.08

• The new beta will be 1.19, close to the required desired beta value of 1.2

The advantages are as follows:

• The portfolio becomes resistant to systematic risk
• Diversification helps investors understand different sectors.
• Such portfolios suit both long-term wealth creation and short-term profits.
• A variety of financial instruments fit this investment strategy.

The disadvantages are as follows:

• This approach is often called Markowitz Mean Variance Model. It is more inclined towards variance and tends to overlook potential risks.
• It does not guarantee good returns and is only based on historical data.
• The model does not account for associated costs like broker commissions, taxes, and other charges.
• The whole model is based on irrelevant stock market assumptions. In reality, stock markets are as unpredictable as they are volatile.

This article has been a guide to What is Markowitz Model. We explain its assumptions, diagram, formula, calculations, example, and advantages and disadvantages. You can learn more about it from the following articles -

• Black Litterman Model
• Portfolio Rebalancing
• Portfolio Management