A Priori Probability

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What is A Priori Probability?

“A Priori Probability,” also known as classical probability. It refers to the probability of those events that can only have a finite number of outcomes, and each outcome is equally likely to occur. In this type of probability, the outcomes are not influenced by their primary outcomes. For example, any outcome drawn today will in no way influence the prediction of the probability of future outcomes.

What is A Priori Probability?

Explanation

The term "a priori" is Latin for the words "presumptive" or "deductive." As the name suggests, it is more deductive and is not influenced by what has happened in the past. In other words, the underlying principle of a priori probability follows logic rather than history to determine the probability of a future event. Typically, one may calculate a classical probability's outcome by rationally evaluating the pre-existing information or circumstance associated with a situation. As mentioned above, in such a probability estimation, each event is independent, and their previous events impact their occurrence in no way.

Formula

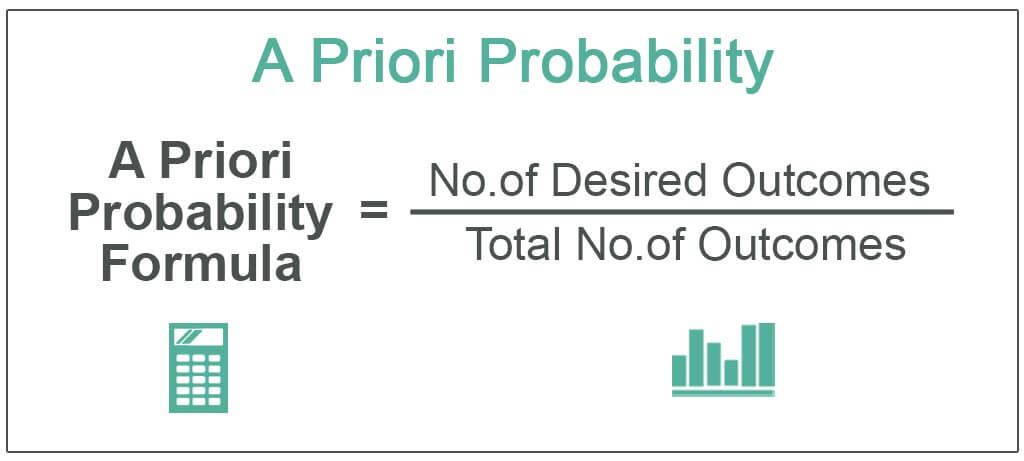
One can express the formula by dividing the number of desired outcomes by the total number of outcomes. Mathematically, it represents as below:

A Priori Probability Formula = No. of Desired Outcomes / Total No. of Outcomes

One should note that one can only use the above formula in the case of events wherein all the outcomes are equally likely to occur and are mutually exclusive.

Examples

Below are examples to understand the concept in a better manner.

Example #1

Let us take the example of a fair dice roll to illustrate the concept. A fair dice has six sides with an equal probability of rolling, and all the outcomes are mutually exclusive. So, first, determine the a priori probability of rolling a 1 or 5 in a fair dice roll.

Given,

No. of desired outcomes = 2 (roll a 1 or 5)
Total no. of outcomes = 6 (roll a 1, 2, 3, 4, 5 or 6)

Solution

Now, one can calculate the probability of rolling a 1 or 5 in a fair dice roll by using the above formula:

= 2 / 6
= 33.3%

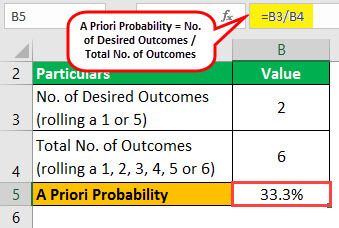
Therefore, the probability of rolling a 1 or 5 in a fair dice roll is 33.3%.

Example #2

Let us take the example of a standard 52-card deck to illustrate the concept. There are 52 cards equally distributed among four suits (13 ranks in each suit) in a typical 52- card deck. If one draws one card and places it back in the deck, then determine it to draw a card from the heart suit.

Given,

No. of desired outcomes = 13 (as each suite has 13 ranks)
Total no. of outcomes = 52

Solution

Now, one can calculate the a priori probability of drawing a card from a hearts suit by using the above formula:

= 13 / 52
= 25.0%

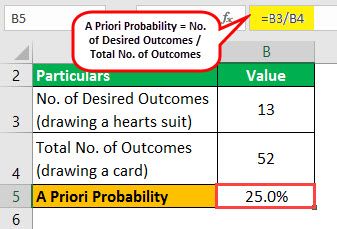
Therefore, the probability of drawing a card from a heart suit from a standard deck is 25.0%.

Example #3

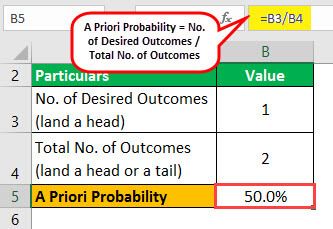
Let us take the example of a coin toss to illustrate the concept. A coin has two sides – a head and a tail. So, first, determine the a priori probability of landing a head in a usual coin toss.

Given,

No. of desired outcomes = 1 (land a head)
Total no. of outcomes = 2 (land a head or a tail)

Solution

Now, one can calculate the probability of landing a head in a coin toss by using the above formula:

= 1 / 2
= 50.0%

Prior Probability vs. A Priori Probability

Advantages

Some of the major advantages are as follows:

The concept of a priori probability is easy to explain.
It is a simple concept that one can apply to many real-life situations.

Drawbacks

Some of the major drawbacks are as follows:

It fails when the probability of occurrence of the events is not equally likely.
One can't use it for cases where the number of outcomes is potentially infinite.

Conclusion

So, one can see that a priori probability is an essential statistical technique that also extends to other concepts. However, it has its limitations that one needs to take cognizance of while drawing statistical insights.