Table Of Contents
What is Probability Density Function?
The probability density function gives the output indicating the density of a continuous random variable lying between a specific range of values. If a given scenario is calculated based on numbers and values, the function computes the density corresponding to the specified range.
The function, when solved, defines the relationship between the random variable and its probability. The variable's probability is matched when the function is solved. The function is denoted by f(x), and the graphical portrayal gives a bell curve. The area between any two particular values gives the outcome probability of the designated observation.
Key Takeaways
- The probability density function (PDF) gives the output indicating the density of a continuous random variable lying between a specific range of values.
- There are imperatively two types of variables: discrete and continuous. The PDF turns into the probability mass function when dealing with discrete variables.
- It is used in statistical calculations and graphically represented as a bell curve forming a relationship between the variable and its probability.
- Its application is significant in machine learning algorithms, analytics, probability theory, neural networks, etc.
Probability Density Function Explained
The probability density function (PDF) is associated with a continuous random variable by finding the probability that falls in a specific interval. A continuous random variable can take an uncountably infinite number of possible values. The probability mass function replaces the PDF for a discrete random variable that takes on finite or countable possible values.
PDFs have a wide range of applications. For example, it is used in modeling and predictions related to chemically reactive turbulent flows and analysis of stock price returns. For each application, the corresponding curve is depicted on a graph, and analyzing bell curve features like symmetry and sides like left or right gives important information.
Another important concept significant in understanding the PDF is the cumulative distribution function. It is also used to explain the distribution of random variables, primarily continuous random variables. The differentiating cumulative distribution function of a continuous random variable will give the value of PDF, and integrating the PDF gives the value of the cumulative distribution function.
Formula
Probability density function formula:
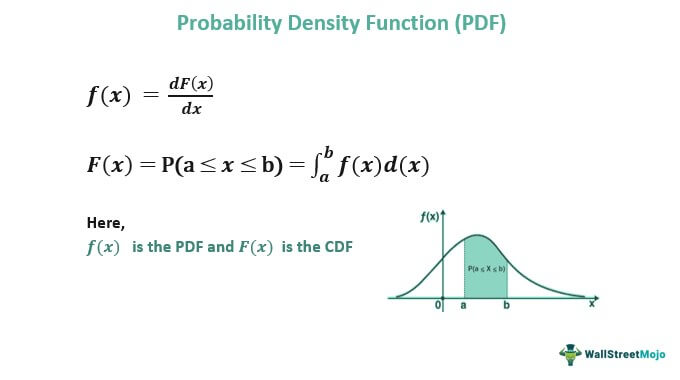
To calculate the PDF online probability density function calculator or formula based on cumulative distribution function is used, we differentiate the cumulative distribution function:
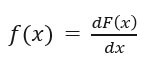
f(x) is the PDF and F(x) is the CDF
or
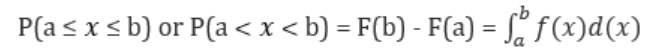
Here,
- X lies between lower limit 'a' and upper limit 'b'
- F(b): Cumulative distribution function at a
- F(a): Cumulative distribution function at b
Examples with Calculation
To better understand the formula and its application, consider the following PDF example:
The PDF is:
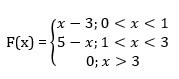
Find P(1<x<2)
The formula is:
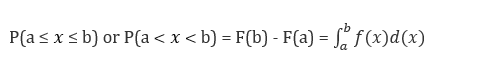
Applying the upper and lower limits:
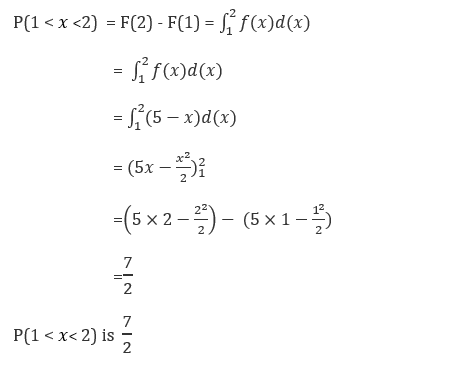
Applications
- It is used in machine learning algorithms, analytics, probability theory, neural networks, etc.
- Calculates probabilities associated with continuous random variables.
- The PDF of stock price returns is used for studying various market scenarios.
- It is used to model various processes and derive solutions to the problem. For example, it is applied to model chemically reacting turbulent flows and derive appropriate resolution to the closure problems.
