Expected Value

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Expected Value in Statistics Definition

Expected Value (EV) is a mathematical calculation that finds the anticipated value of an investment based on various possibilities taken into consideration (like the change in the value from time to time and the period for which the price). One can calculate it using the outcomes and the likelihood of these outcomes occurring. It helps an investor to zero in on the most beneficial investment.

The formula for expected value is simple:

Expected Value = ∑ Px * X

Expected Value in Statistics Definition

Expected Value (EV) is a mathematical calculation used to determine the anticipated value of an investment by considering different possibilities and their corresponding probabilities.
It aids investors in making informed decisions by identifying the most advantageous investment option.
The formula for expected value is ∑ Px * X, where Px represents the probability distribution, and X represents the outcomes.
Expected value supports decision-making for investors and managers based on the expected return on investment (ROI), identifies potential underperforming investments, combines multiple outcomes for easier decision-making, and can be easily calculated by individuals with basic mathematical skills.

Expected-Value — Image Showing Expected Value (EV) in Statistics Formula

Px = Probability distribution
X = Outcomes

Examples of EV

Below are some examples of the expected value.

Example #1

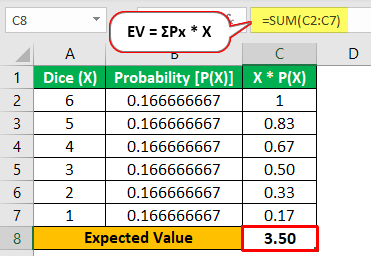
The best example to understand the expected value is the dice. A dice has 6 sides, and the probability of getting a number between 1 to 6 is 1/6.
If we assume X as the outcome of a rolled dice, X is the number that appears on the top of the rolled dice.
Since we are not given the probability of the numbers, we will go ahead with the probability of 1/6 in our calculations.

The calculation for EV will be as below:

Example #2

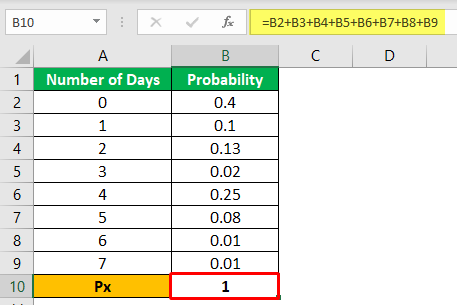
The below-given table shows the number of days you’ll go to the gym and its probability.

If you see, add up the probability in the table above.

Since it is given the probability in this case, we can directly calculate the expected value by multiplying the number of days with the probability.

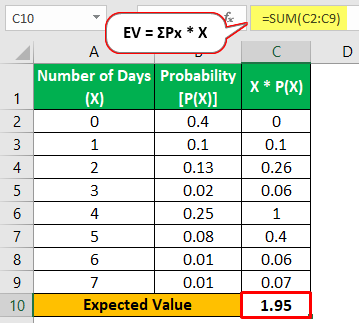
According to the above information, the expected number of days to head to the gym is roughly two days a week. As per the calculation, it is 1.95, so you can say that in 20 weeks, you went to the gym 39 times (1.95 * 20).

There might be weeks when you didn’t visit the gym and weeks when you went on all seven days. It helps to understand that even though the distribution of days attending the gym might not be constant, it is still possible to get a rough estimate.

Advantages

Helps investors and managers in deciding on projects based on expected ROI.
Highlights red flags in case an investment is going to underperform.
Various outcomes are combined to arrive at a single outcome, which eases decision-making.
The easy calculation makes it accessible for anyone with basic mathematical skills to calculate the expected value.
Consider every possibility of outcome to calculate the expected value.

Disadvantages

It is based on mathematical calculations and is a numerical representation of the future value of any investment.
The EV depends on probability, which is highly subjective.
It is an average of all possible outcomes. Hence, it does not give the actual result or outcome.
One cannot use it for a one-time activity but scenarios with repeated outcomes.
It does not give a view of the risk involved.
It may not correspond to any of the possible outcomes.

Important Points

In probability, the expected value is the weighted average of all possible outcomes with the weights given by the theoretical probabilities. It is represented by E(x).
It is not recommended for a one-time or infrequent scenario since EV derives from various trials.
It provides a fair idea of the future value of an investment.
EV is not foolproof, yet the result obtained from the calculation can prove useful during decision-making.

Conclusion

It is the future value of an investment or a product based on various possibilities, like the change in the value from time to time and the period for which the price is considered.
It is calculated mathematically by multiplying the outcomes with a probability distribution and adding them.
The EV can differ from the calculated expected value since it is based on assumptions. Still, it can provide a pathway to understanding roughly where the expected value will be.
Investors can rely on expected value to decide whether investing is worthy and can reap the maximum out of their investment.

Frequently Asked Questions (FAQs)

1. What are the assumptions followed in the expected value method?

The expected value method assumes that the probabilities assigned to each outcome are accurate and reflect the true likelihood of occurrence. It also assumes that the outcomes are independent of each other.

2. What are the applications of expected value?

Expected value is widely used in various fields such as finance, economics, decision analysis, and statistics. It is applied in investment analysis, project evaluation, insurance calculations, gambling, and decision-making under uncertainty.

3. What is the expected value vs. the mean?

Expected value and meaning are closely related concepts. The expected value represents the long-term average value of a random variable, calculated by multiplying each possible outcome by its probability and summing them. The mean, on the other hand, is simply the arithmetic average of a set of values. In some cases, the expected value and mean may refer to the same concept, while in others, they may differ depending on the context.