Hypergeometric Distribution

What Is Hypergeometric Distribution?

Hypergeometric distribution is a distinct probability distribution that defines the k successes probability (some random draws for the object drawn that has some specified feature) in n no of draws, without any replacement, from a given population size N that includes accurately K objects having that feature, where the draw may succeed or may fail.

You are free to use this image o your website, templates, etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Hypergeometric Distribution (wallstreetmojo.com)

The probability of a hypergeometric distribution is derived using the number of items in the population, number of items in the sample, number of successes in the population, number of successes in the sample, and few combinations.

What Is Hypergeometric Distribution?

In statistics and the probability theory, hypergeometric distribution means a distinct distribution that displays the k successes probability in n no of draws, without any replacement, from a given population size N. The length N includes precisely K objects with that feature, where the interest may succeed or fail.
The hypergeometric distribution probability can be obtained utilizing the number of items in the population, number of items in the sample, number of successes in the population, number of wins in the model, and few combinations.
The hypergeometric distribution concept is essential because it accurately analyzes the probabilities when the number of trials is not very large and when samples are considered from a finite population without replacement

Hypergeometric Distribution Explained

Hypergeometric distribution plays a vital role in statistics and probability theory as it helps make selections from two groups without replacing the members of those groups. To see how to calculate it, let us follow the below steps:

Firstly, determine the total number of items in the population, which is denoted by N. For example, the number of playing cards in a deck is 52.
Next, determine the number of items in the sample, denoted by n—for example, the number of cards drawn from the deck.
Next, determine the instances which will be considered to be successes in the population, and it is denoted by K. For example, the number of hearts in the overall deck, which is 13.
Next, determine the instances which will be considered to be successes in the sample drawn, and it is denoted by k. E.g., the number of hearts in the cards drawn from the deck.
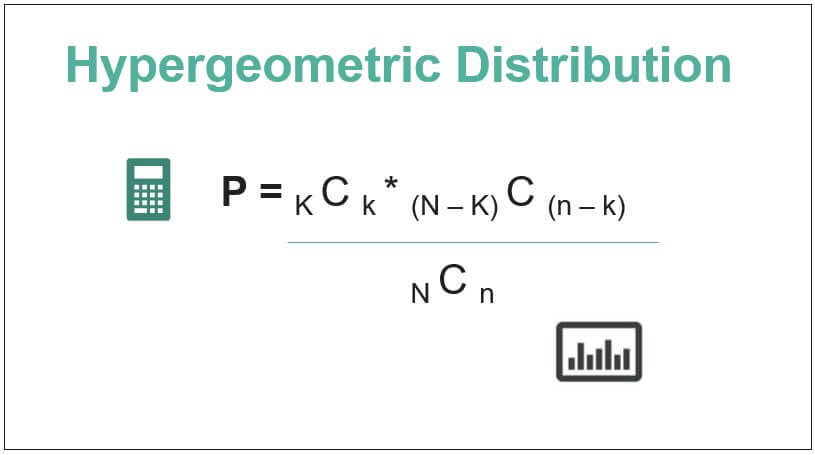
Finally, the formula for the probability of a hypergeometric distribution is derived using several items in the population (Step 1), the number of items in the sample (Step 2), the number of successes in the population (Step 3), and the number of successes in the sample (Step 4) as shown below.

P = _KC _k* _{(N – K)}C _{(n – k)}/_NC _n

Formula

Mathematically, the hypergeometric distribution for probability is represented as:

P = _KC _k* _{(N – K)}C _{(n – k)}/_NC _n

where,

N = No. of items in the population
n = No. of items in the sample
K = No. of successes in the population
k = No. of successes in the sample

The mean and standard deviation of a hypergeometric distribution are expressed as,

Mean = n * K / N

Standard Deviation = [n * K * (N – K) * (N – n) / {N² * (N – 1)}]^1/2

Examples

Let us consider the following hypergeometric distributions examples to check how it works:

You can download this Hypergeometric Distribution Excel Template here – Hypergeometric Distribution Excel Template

Example #1

Let us take the example of an ordinary deck of playing cards from where 6 cards are drawn randomly without replacement. First, determine the probability of drawing exactly 4 red suit cards, i.e., diamonds or hearts.

Given N = 52 (since there are 52 cards in an ordinary playing deck)
n = 6 (Number of cards drawn randomly from the deck)
K = 26 (since there are 13 red cards each in diamonds and hearts suit)
k = 4 (Number of red cards to be considered successful in the sample drawn)

Solution:

Therefore, the calculation of the probability of drawing exactly 4 red suits cards in the draw 6 cards using the above formula is as follows:

Hypergeometric Distribution Formula Example1

Probability = _KC _k* _{(N – K)}C _{(n – k)}/_NC _n

= ₂₆C ₄* _{(52 – 26)}C _{(6 – 4)}/₅₂C ₆ = ₂₆C ₄* ₂₆C ₂/₅₂C ₆

= 14950 * 325 / 20358520

The probability will be –

Probability = 0.2387 ~ 23.87%

Therefore, there is a 23.87% probability of drawing exactly 4 red cards while drawing 6 random cards from an ordinary deck.

Example #2

Let us take another example of a wallet that contains 5 $100 bills and 7 $1 bills. If 4 bills are chosen randomly, then determine the probability of choosing exactly 3 $100 bills.

Given, N = 12 (Number of $100 bills + Number of $1 bills)
n = 4 (Number of bills chosen randomly)
K = 5 (since there are 5 $100 bills)
k = 3 (Number of $100 bills to be considered a success in the sample chosen)

Solution:

Therefore, the calculation of the probability of choosing exactly 3 $100 bills in the randomly chosen 4 bills using the above formula is as follows:

Hypergeometric Distribution Formula Example2

Probability = _KC _k* _{(N – K)}C _{(n – k)}/_NC _n

= ₅C ₃* _{(12 – 5)}C _{(4 – 3)}/₁₂C ₄ = ₅C ₃* ₇C ₁/₁₂C ₄

= 10 * 7 / 495

The probability will be –

Probability = 0.1414 ~ 14.14%

Therefore, there is a 14.14% probability of choosing exactly 3 $100 bills while drawing 4 random bills.

When To Use?

The concept of hypergeometric distribution is important because it provides an accurate way of determining the probabilities when the number of trials is not very large and when samples belong to a finite population without replacement. The hypergeometric distribution is analogous to the binomial distributionBinomial Distribution The Binomial Distribution Formula calculates the probability of achieving a specific number of successes in a given number of trials. nCx represents the number of successes, while (1-p) n-x represents the number of trials.read more, used when the number of trials is substantially large. However, hypergeometric distribution is all about sampling without replacement.

Hypergeometric Distribution Vs Binomial Distribution

Both these types of distributions help identify the probability or chances of an event occurring a specific number of times in n number of trials. However, they still differ. Let us look at the differences between the two:

Category	Hypergeometric Distribution	Binomial Distribution
Replacement	Replacement of group members does not occur	Replacement of group members occurs
Variation	The probability changes with every trial.	The probability remains constant with every trial.
Usage	Used in a population small as the outcome has a large effect on the probability of a situation being an event or non-event.	Used in a population large enough for the outcome to have an effect on the probability of a situation being an event or non-event.

Frequently Asked Questions (FAQs)

What is the difference between binomial and hypergeometric distribution?

In the binomial distribution, the probability is similar for every trial. In comparison, in the hypergeometric distribution, each shot changes the probability for each subsequent trial as there is an absence of replacement.

How to identify hypergeometric distribution?

One may identify the hypergeometric distribution by population size, event count in population, and sample size.

Is hypergeometric distribution independent?

One may use the Hypergeometric Distribution while performing multiple trials like the Binomial Distribution. In addition, one may also count the number of “successes” and “failures.” The main difference is the trials are based on each other.

Can hypergeometric distribution be negative?

N, M, and m are non-negative integers that meet the condition m≤M≤N. In addition, a negative hypergeometric distribution often comes in a sampling scheme without replacement.

Hypergeometric Distribution

What Is Hypergeometric Distribution?

Table of contents