Addition Rule Of Probability

The addition rule for probability is a fundamental principle in probability theory that finds the possibility of the occurrence of at least one of two or more mutually exclusive or not mutually exclusive events if not all. It is also known as the "OR" rule in probability.

The addition rule of probability can be applied in finance to determine the probability of different events, such as the likelihood of a stock price increasing or decreasing or the probability of a company meeting its financial targets. By calculating the probability of multiple events, investors and financial analysts can make more informed investment decision and risk management.

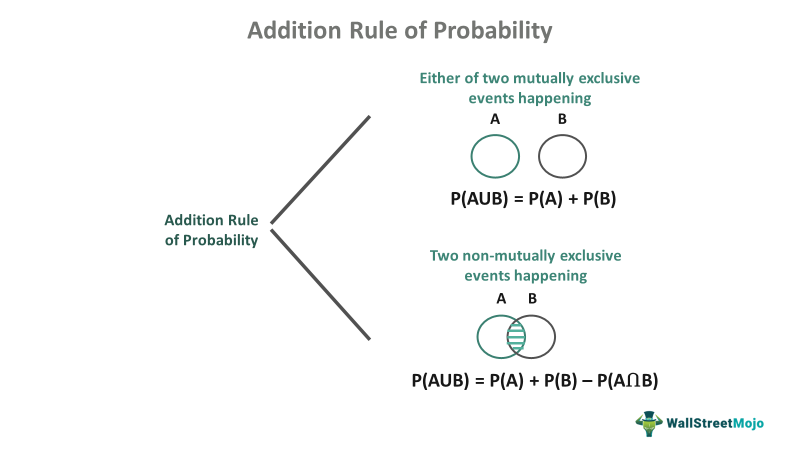
• The addition rule for probability, addition theorem, or "OR" rule determines the chances that one or more events will occur when a sample space contains multiple events.
• For mutually exclusive events, P(A or B) = P(A) + P(B); however, for events that are not mutually exclusive, P(A or B) = P(A) + P(B) - P(A and B), where P(A and B) is the probability of the intersection of events A and B.
• The addition rule for probability can be marked on a Venn Diagram separately for the event that is mutually exclusive or not mutually exclusive.

The addition rule for probability is one of the six probability theorems that work where we need to determine the chances that any of the given events may occur. For example, if there are two events, A and B, then the addition theorem of probability is represented as P(A or B) or P(A ∪ B). The addition law of probability is also called the "OR" rule since it gauges the possibility of events A or B. Probability is a mathematical concept that gauges the chances of the happening of a random event.

Given below are the various terminologies used in probability:

1. Event: An event is a conclusion or outcome of an experiment.
2. Sample space: It denotes all the possible outcomes or events.
3. Mutually exclusive events: All the possible events of an experiment that cannot occur simultaneously or together.
4. Not mutually exclusive or Mutually exhaustive events: It represents all those possible events that can happen simultaneously.
5. Independent events: Independent events don't rely on the occurrence of other events.

The relationship between the events can be depicted using a Venn diagram. If events A and B are mutually exclusive, the addition rule calculates the probability of either event A or B occurring. However, if events A and B are not mutually exclusive, the addition rule determines the probability of either event A, event B, or both.

The addition rule for probability can be applied in two ways depending upon the type of events, i.e., whether they are mutually exclusive or exhaustive when multiple events are assumed.

1. Addition Rule For Mutually Exclusive Events

When A and B are mutually exclusive events:

P(A or B) = P(A) + P(B) or, P(A ∪ B) = P(A) + P(B)

2. Addition Rule For Not Mutually Exclusive Events

Say A and B are mutually exhaustive or not mutually exclusive events:

P(A or B) = P(A) + P(B) - P(A and B) or, P(A∪B) = P(A) + P(B) - P(A ∩ B); 

Where P(A and B) or, P(A ∩ B) = P(A) * P(B)

The addition rule of probability in finance calculates the probability of one or more events occurring when a sample space contains multiple events. It can be applied in various financial scenarios, such as in calculating the probability of default for a portfolio of loans or determining the likelihood of multiple events impacting the value of a stock or portfolio.

The addition rule is particularly useful when analyzing the risk of different investment scenarios. It allows investors to assess the likelihood of multiple outcomes and adjust their investment strategies accordingly. Additionally, it can be used in risk management strategies, such as calculating the probability of losses exceeding a certain threshold.

The addition rule of probability is a powerful tool for financial analysis and decision-making, helping investors and financial professionals make more informed decisions in an uncertain and dynamic market environment.

Check out these examples to get a better idea:

Example #1

Suppose an investor considers investing in two stocks, A and B. The probability of stock A increasing in value over the next year is 0.4, and the probability of stock B increasing in value over the next year is 0.6. The investor wants to know the probability that at least one of the two stocks will increase in value. By using the addition rule of probability, we can calculate the probability as follows:

P(A or B) = P(A) + P(B) - P(A and B)

= 0.4 + 0.6 - (0.4 x 0.6)

= 0.76

So, there is a 76% probability that at least one of the two stocks will increase in value over the next year.

Example #2

Let's say a bank is considering giving loans to two borrowers, X and Y. The probability of borrower X defaulting on the loan is 0.3, and the probability of borrower Y defaulting on the loan is 0.4. The bank wants to know the probability that at least one borrower will default. By using the addition rule of probability, we can calculate the probability as follows:

P(X or Y) = P(X) + P(Y) - P(X and Y)

= 0.3 + 0.4 - (0.3 x 0.4)

= 0.58

So, there is a 58% probability that at least one borrower will default on the loan.

This has been a guide to what is Addition Rule Of Probability. We explain the topic in detail, including its examples, formula, and how to use it. You can learn more about it from the following articles –

• Conditional Probability
• Subjective Probability
• Empirical Probability