Alpha Formula

Publication Date :

21 Feb, 2019

Blog Author :

Edited by :

Reviewed by :

Download FREE Alpha Formula Excel Template and Follow Along!

Alpha Formula Excel Template.xlsx

Table Of Contents

Formula to Calculate Alpha of a Portfolio

Alpha is an index that is used for determining the highest possible return concerning the least amount of risk, and according to the formula, alpha is calculated by subtracting the risk-free rate of the return from the market return and multiplying the resultant with the systematic risk of the portfolio represented by the beta and further subtracting the resultant along with the risk-free rate of the return from the expected Rate of the return on the portfolio.

Alpha Formula Equation

The alpha calculation formula can be used first by calculating the expected rate of return of the portfolio based on the risk-free rate of return, a beta of the portfolio, and market risk premium, then deducting the result from the actual rate of return of the portfolio.

Alpha of portfolio = Actual rate of return of portfolio - Expected Rate of Return on Portfolio

Alpha of portfolio = Actual rate of return of portfolio - Risk-free rate of return - β * (Market return - Risk-free rate of return)

Key Takeaways

The alpha formula evaluates a portfolio's risk-mitigated performance by quantifying excess or aberrant returns compared to a benchmark.
Active managers strive to generate alpha, diminishing idiosyncratic risks in a diversely composed portfolio.
Alpha is a metric that seeks to optimize returns relative to risk. It is achieved by deducting the risk-free rate from the market return, multiplying it by beta, and subtracting this from the projected portfolio return.
In financial frameworks such as the CAPM (Capital Asset Pricing Model), alpha serves as a pivotal gauge to ascertain the utmost attainable return from an investment while mitigating risk.
It's also synonymous with the Jensen Index.

Alpha of a Portfolio Calculation (Step by Step)

Firstly, figure out the risk-free rate, which can be determined from the average annual return of government security, say Treasury bonds, over a substantial period.
Next, figure out the market return, which can be done by tracking the average annual return of a benchmark index, say the S&P 500, over a substantial period. Consequently, the market risk premium is computed by deducting the risk-free rate of return from the market return.
Market risk premium = Market return – Risk rate of return
Next, the beta of a portfolio is determined by assessing the portfolio's movement compared to the benchmark index.
Now, based on the risk-free rate of return (step 1), a beta of the portfolio (step 3), and market risk premium (step 2), the expected rate of return of the portfolio is calculated as below.
Expected rate of return of portfolio = Risk-free rate of return + β * (Market return – Risk-free rate of return)
Next, the actual rate of return achieved by the portfolio is calculated based on its current value and the previous value.
Finally, the formula for calculation of alpha of the portfolio is done by deducting the expected rate of return of the portfolio (step 4) from the actual rate of return of the portfolio (step 5) as above.

Examples

Let us take the example of a mutual fund that has realized a return of 16% during the last year. The appropriate benchmark index for the fund has an annual book return of 11%. Further, the beta of the mutual fund vis-à-vis the benchmark index is 1.3while the risk-free rate of return is 4%. Do the calculation of the alpha of the mutual fund.

The following is the data for calculating the alpha formula per the question.

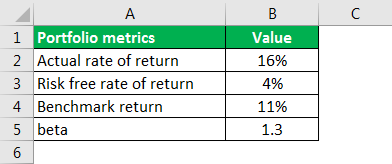
Expected Rate of Return

Expected rate of return = Risk-free rate of return + β * (Benchmark return – Risk-free rate of return)

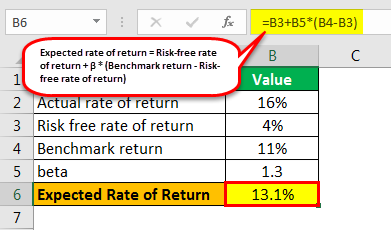
= 4% + 1.3 * (11% - 4%)
= 13.1%

Therefore, the Calculation of the Alpha of the mutual fund will be as follows –

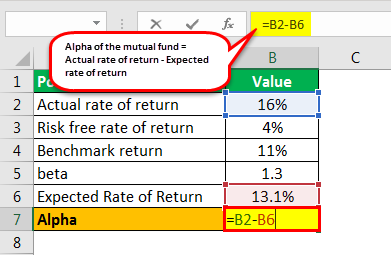
Alpha of the mutual fund = Actual rate of return – An expected rate of return
Alpha = 16% - 13.1%

Alpha Calculation of Mutual Funds

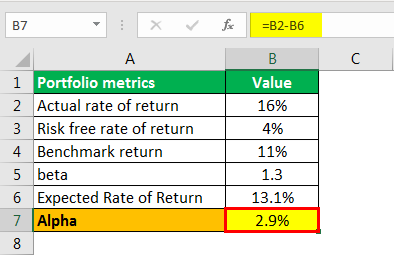
Alpha = 2.9%

The alpha of the mutual fund is 2.9%.

Relevance and Uses of Alpha Formula

The term alpha refers to the index used in many financial models, such as the CAPM (capital asset pricing model), to assess the highest possible return from an investment with the least risk. Alpha is also known as Jensen Index.
It is essential to understand the concept of the alpha formula because it is used to measure the risk-adjusted performance of a portfolio.
It is also recognized as the excess return or the abnormal rate of return of a portfolio. The figure demonstrates how much worse or better a fund had performed concerning a benchmark. This variance is then credited to the judgments made by the fund manager. Active portfolio managers predominantly strive to generate alpha in a diversified portfolio (diversification is intended to eliminate unsystematic risk).