Risk Adjusted Return

Risk-adjusted return is a technique to measure and analyze the returns on an investment for which the financial, market, credit and operational risksOperational RisksOperational risk is the business uncertainty a company comes across in the industry while executing its everyday business operations. Such risks arise due to internal system breakdown, technical issues, external factors, managerial problems, human errors or information gap. read more are analyzed and adjusted so that an individual can take a decision on whether the investment is worth it with all the risks it poses to the capital invested.

Why do we invest in money? Simple. To reap returns. But have we ever thought if the return is justified enough for the underlying risk factors? While people usually have this perception about money-generating returns, the risk is ab oft-forgotten element. Returns are nothing but the gains on the invested surplus: the differential money earned. In purely economic terms, it is a method of considering profits in relation to capital invested.

In this article, we discuss Risk-Adjusted Returns in Detail –

• How is risk defined?
• Risk-adjusted returns and its importance
• #1 – Sharpe’s Ratio (Risk Adjusted Return)
• #2 – Treynor Ratio (Risk Adjusted Return)
• #3 – Jensen’s Alpha (Risk Adjusted Return)
• #4 – R-Squared (Risk Adjusted Return)
• #5 – Sortino Ratio (Risk Adjusted Return)
• #6 – Modigliani Risk Adjusted Performance
• Risk Adjusted Returns – Sharpe Ratio vs Treynor Ratio vs Jensen’s Alpha
• Conclusion

How is risk defined?

The standard definition for investment risk is deviance from an expected outcome. It can be expressed in absolute terms or in relation to something such as a market benchmark. That deviation can either be positive or negative. If an investor plans to achieve higher returns, in the long run, they have to be more open to short-term volatility. The quantum of volatility depends on the risk tolerance of an investor. Risk tolerance is nothing but the propensity to take on volatility for specific financial circumstances, considering their psychological, mental ease with uncertainty and the probability of incurring large short-term losses.

Risk-adjusted returns and its importance

Risk-adjusted return fine-tunes an investment’s return by measuring how much risk is involved in producing that return.  Investment Portfolios are made up of positions in stocks, mutual funds, and ETFs. The concept of risk-adjusted return is used to compare the returns of portfolios with different risk levels against a benchmark with a known return and risk profile.

If an asset has a lower risk quotient than the market, the return of the asset above the risk-free rate is considered a big gain.  If the asset depicts a higher than market risk level, the risk-free differential return is reduced.

Risk-adjusted returns are crucial as it helps to solve three major problems:

You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Risk Adjusted Return (wallstreetmojo.com)

There are mainly six most widely-used methods of calculating risk-adjusted returns. We look at them in detail below –

You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Risk Adjusted Return (wallstreetmojo.com)

#1 – Sharpe’s Ratio (Risk Adjusted Return)

The Sharpe ratio meaningSharpe Ratio MeaningSharpe Ratio, also known as Sharpe Measure, is a financial metric used to describe the investors’ excess return for the additional volatility experienced to hold a risky asset. You can calculate it by, Sharpe Ratio = {(Average Investment Rate of Return – Risk-Free Rate)/Standard Deviation of Investment Return} read more symbolizes how well the return of an asset compensates the investor for the risk taken. When comparing two assets against a common benchmark, the one with a higher Sharpe ratio provides a better return for the same risk (or, equivalently, the same return for lower risk). Developed by Nobel Prize winner William F. Sharpe in 1966, the Sharpe ratio is defined as the average return earned in excess of the risk-free rate per unit of volatility or total risk i.e., standard deviation. The Sharpe ratio has become the most widely used method for calculating risk-adjusted returns; however, it can only be accurate if the data has a normal distributionNormal DistributionNormal Distribution is a bell-shaped frequency distribution curve which helps describe all the possible values a random variable can take within a given range with most of the distribution area is in the middle and few are in the tails, at the extremes. This distribution has two key parameters: the mean (µ) and the standard deviation (σ) which plays a key role in assets return calculation and in risk management strategy.read more.

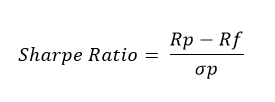
• Rp = Expected Portfolio Return
• Rf – Risk Free Rate
• Sigma(p) = Portfolio Standard Deviation

The Sharpe ratio can also help determine whether a security’s excess returns are a result of prudent investment decisions or just too much risk. Even as one fund or security can reap higher returns than its counterparts, the investment can be considered good if those higher returns are free from an element of additional risk. The more the Sharpe ratio, the better is its risk-adjusted-performance.

Sharpe Ratio Example

Let’s assume that the 10-year annual return for the S&P 500 (market portfolio) is 10%, while the average annual return on Treasury bills (a good proxy for the risk-free rate) is 5%. The standard deviation is 15% over a 10-year period.

Managers	Average Annual Return	Portfolio Standard Deviation	Rank
Fund A	10%	0.95	III
Fund B	12%	0.30	I
Fund C	8%	0.28	II

• Market = (.10-.05)/0.15 =0.33
• (Fund A) = (0.10-.05)/0.95= 0.052
• (Fund B) = (0.12-.05)/0.30 = 0.233
• (Fund C) = (.08-.05)/0.28 = .0.107

#2 – Treynor Ratio (Risk Adjusted Return)

Treynor is a measurement of the returns earned in excess of that which could have been earned on an investment that has no diversifiable riskDiversifiable RiskA diversifiable risk refers to the firm-specific uncertainty that impacts an individual stock price rather than affecting the whole industry or sector in which the firm operates. Such risk can be mitigated or reduced by adopting diversification strategies to ensure that the returns are not affected.read more. In short, it is also a reward-volatility ratio, just like the Sharpe’s ratio, but with just one difference. It uses a beta coefficientUses A Beta CoefficientThe beta coefficient reflects the change in the price of a security in relation to the movement in the market price. The Beta of the stock/security is also used for measuring the systematic risks associated with the specific investment.read more in place of standard deviations.

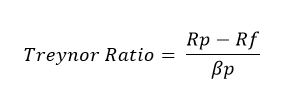
• Rp = Expected Portfolio Return
• Rf – Risk Free Rate
• Beta(p) = Portfolio Beta

This ratio developed by Jack L. Treynor determines how successful an investment is in providing investors compensation, with consideration for the investment’s inherent level of risk. The Treynor ratioTreynor RatioThe Treynor ratio is similar to the Sharpe ratio and it calculates excess return over risk-free return per unit of portfolio volatility using beta rather than standard deviation as a risk measure. As a result, it gives the excess return over the risk-free rate of return per unit of the beta of the investor's overall portfolio.read more depends upon Beta – which depicts the sensitivity of an investment to movements in the market – to evaluate the risk. The Treynor ratio is based on the premise that risk, an integral element of the entire market (as represented by Beta) must be fined because diversification cannot eliminate it.

When the value of the Treynor ratio is high, it is a sign that an investor has generated high returns on each of the market risks he has assumed. The Treynor ratio helps one to understand how each investment within a portfolio is performing. This way, the investor also gains an idea as to how efficiently capital is being utilized.

Also, check out CAPM BetaCAPM BetaCAPM Beta is an essential theoretical measure of how a single stock moves with respect to the market. In this method, we determine the cost of equity by summing up the beta and risk premium product with the risk-free rate.read more

Treynor Ratio Example

Let’s assume that the 10-year annual return for the S&P 500 (market portfolio) is 10%, while the average annual return on Treasury bills (a good proxy for the risk-free rate) is 5%.

Managers	Average Annual Return	Beta	Rank
Fund A	12%	0.95	II
Fund B	15%	1.05	I
Fund C	10%	1.10	III

• Market = (.10-.05)/1 = .05
• (Fund A) = (.12-.05)/0.95 = .073
• (Fund B) = (.15-.05)/1.05 = .095
• (Fund C) = (.10-.05)/1.10 = .045

#3 – Jensen’s Alpha (Risk Adjusted Return)

Alpha is often considered an active return on investment. It determines the performance of an investment against a market index used as a benchmark, as they are often considered to represent the market’s movement as a whole. The excess returns of a fund as compared to the return of a benchmark index is the fund’s Alpha. Basically, the alpha coefficient indicates how an investment has performed after accounting for the risk it involved:

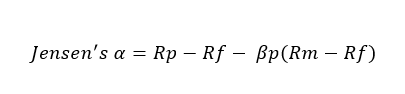
• Rp = Expected Portfolio Return
• Rf – Risk-Free Rate
• Beta(p) = Portfolio Beta
• Rm = Market Return

Alpha<0: the investment has earned too little for its risk (or was too risky for the return)

Alpha=0: the investment has earned a return adequate for the risk taken

Alpha>0: the investment has a return in excess of the reward for the assumed risk

Jensen’s Alpha Example

let us assume a portfolio realized a return of 17% in the previous year. The approximate market index for this fund returned 12.5%. The Beta of the fund versus the same index is 1.4, and the risk-free rate is 4%.

Thus, Jensen’s Alpha = 17 – [4 + 1.4 *(12.5-4)]

= 17 – [4 + 1.4* 8.5] = = 17 – [4 + 11.9]

= 1.1%

Given the Beta of 1.4, the fund is expected to be risky than the market index and thus earn more. A positive alpha is an indication that the portfolio manager earned substantial returns to be compensated for the additional risk taken over the course over the year. If the fund had returned 15%, the computed Alpha would be -0.9%. A negative alpha indicates that the investor was not earning enough returns for the quantum of risk, which was borne.

#4 – R-Squared (Risk-Adjusted Return)

R-squared is a statistical measure that represents the percentage of a fund or security’s movements that is based on the movements in a benchmark index.

• R-squared values range from 0 to 1 and are commonly stated as percentages from 0 to 100%.
• An R-squared of 100% means all movements of security can be completely justified by movements in the index.
• A high R-squared, between 85% and 100%, indicates the fund’s performance patterns reflect that of the index.

However, strong outperformance, coupled with a very low R-Squared ratio, will mean more analysis is required to identify the reason for outperformance.

#5 – Sortino Ratio (Risk Adjusted Return)

Sortino ratioSortino RatioThe Sortino ratio is a statistical tool used to evaluate the return on investment for a given level of bad risk. It is calculated by subtracting the risk-free rate of return from the expected return and dividing the result by the negative portfolio's standard deviation (downside deviation).read more is a variation of the Sharpe ratio. Sortino takes the portfolio’s return and divides this by the portfolio’s “Downside risk”Downside Risk is a statistical measure to calculate the loss in a security’s value due to variations in the market conditions. Also, it refers to the uncertainty level of realized returns being much lesser than the anticipated ones. read more Downside risk is the volatility of returns below a specified level, usually the portfolio’s average return or returns below zero. Sortino shows the ratio of return generated “per unit of downside risk.”

Standard deviationStandard DeviationPortfolio standard deviation refers to the portfolio volatility calculated based on three essential factors: the standard deviation of each of the assets present in the total portfolio, the respective weight of that individual asset, and the correlation between each pair of assets of the portfolio.read more includes both the upward as well as downward volatility. However, most investors are primarily concerned about the downward volatility. Therefore, the Sortino ratio depicts a more realistic measure of the downside risk embedded in the fund or the stock.

• Rp = Expected Portfolio Return
• Rf – Risk-Free Rate
• Sigma(d) = Standard Deviation of Negative Asset Returns

Sortino’s Ratio Example

Let’s assume Mutual FundMutual FundA mutual fund is a professionally managed investment product in which a pool of money from a group of investors is invested across assets such as equities, bonds, etcread more A has an annualized return of 15% and a downside deviation of 8%. Mutual Fund B has an annualized return of 12% and a downside deviation of 5%. The risk-free rate is 2.5%.

The Sortino ratios for both funds would be calculated as:

• Mutual Fund X Sortino = (15% – 2.5%) / 8% = 1.56
• Mutual Fund Z Sortino = (12% – 2.5%) / 5% = 1.18

#6 – Modigliani Risk-Adjusted Performance

Also known as Modigliani-Modigliani measure or M2, it is used for arriving at the risk-adjusted return of an investment portfolio. It is used for measuring the return from a portfolio adjusted for the risk of the fund/portfolio relative to that of a benchmark (e.g., a specific market or index). It has taken its share of inspiration from the widely accepted Sharpe Ratio; however, it has the significant advantage of being in units of percent return, which makes it easier to interpret.

M2 = R_p – R_m

• Rp is the return on the adjusted portfolio
• Rm is a return on the market portfolio

The adjusted portfolio is the portfolio under management to be adjusted in such a way that it has a total risk as to the market portfolio. The adjusted portfolio is constructed as a combination of the managed portfolio and risk-free asset where weights are assigned according to the risk borne.

The Sharpe ratio can be lead to misleading interpretation when it is negative, and is also difficult to directly compare the Sharpe ratio of several instruments. For instance, if we have one Sharpe ratio of 0.50% and another portfolio with a ratio of -0.50%, the comparison may not make sense between the two portfolios. It is easy to recognize the magnitude of the difference between investment portfolios, which have M2 values of 5.2% and 5.8%. The difference of 0.6% is the risk-adjusted return for the year with the riskiness adjusted to that of the benchmark portfolio.

Risk-Adjusted Returns – Sharpe Ratio vs Treynor Ratio vs Jensen’s Alpha

The Treynor ratio, like the Sharpe ratio, is most effectively used as a ranking tool rather than on an individual basis. Investors can compare funds or portfolios of funds with different amounts of market riskMarket RiskMarket risk is the risk that an investor faces due to the decrease in the market value of a financial product that affects the whole market and is not limited to a particular economic commodity. It is often called systematic risk.read more to determine how they rank according to risk-adjusted return. The ratio is particularly useful when the portfolios or funds that are compared are benchmarked to the same market index or when a fund is compared with its own benchmark index.

As compared with the Sharpe ratio, the value of the Treynor ratio is relative: Higher is better. Jensen’s Alpha, on the other hand, can be used only in an absolute context. The sign and size of Alpha reflect the fund manager’s skills and expertise. However, for any measure to be effective, the benchmark index must be chosen appropriately for the portfolio under consideration.

Many a time a manager may appear expert on a reward-to-systematic-risk basis but unskilled on a reward-to-total-risk basis. An investor comparing the Treynor ratio and the Sharpe ratio of a fund has to understand that a major difference between the two can actually be indicative of a portfolio with a significant proportion of characteristic risk in relation to the total risk. On the other hand, a fully diversified portfolio will be ranked identically according to the two ratios.

Jensen’s Alpha

Managers	Average Annual Return	Beta	Rank
Fund A	12%	0.95	II
Fund B	15%	1.05	I
Fund C	10%	1.10	III

First, we calculate the portfolio’s expected return:

• ER (A) =0.05+0.95*(0.1-0.05) =0.0975 or 9.75%
• ER (B) =0.05+1.05*(0.1-0.05) =0.1030 or 10.30% return
• ER (C) ==0.05+1.1*(0.1-0.05) =0.1050 or 10.50% return

Then, we calculate the portfolio’s Alpha by subtracting the expected return of the portfolio from the actual return:

• Alpha A = 12%- 9.75% = 2.25%
• Alpha B = 15%- 10.30% = 4.70%
• Alpha C = 10%- 10.50% = -0.50%

Conclusion

Risk-adjusted return is used in order to measure that how much return an investment portfolio is generating in comparison to the risk involved, which is expressed generally as a number, and the same can be applied to investment funds, individual securities, and the investment portfolios, etc.

Risk-adjusted return varies from person to person and depends on a plethora of factors such as risk tolerance, availability of funds, readiness for holding a position for a long time for market recovery. In case the investor commits a judgment mistake, the opportunity cost of investors and his tax condition will also be ascertained.

There are various ways in which an investor can improve his risk-adjusted return. One of the most common ways is by adjusting his stock position as per the market volatility. An increase in volatility will usually lead to a decrease in the equities position or vice versa. Fund managers increasingly adopt this strategy to elude large losses and to emphasize maximizing the gains.

However, these measures are do not calculate the risk-adjusted return on a real-time basis. Most of these ratios tend to use the historical risk in a calculation. This is one of the fundamental loopholes that most experts point out. In real life, there can be many latent and unobserved risks that can alter the ranking of investments. One can never calculate the exact risk-adjusted return due to the absence of specific rules. The underlying phenomenon of the use of the risk-adjusted rate of return is that an investor can basically rank them from lowest to highest in terms of attractiveness.

Recommended Articles

This has been a guide to what is Risk Adjusted Return and its meaning. Here we discuss the top 8 importance of risk-adjusted return along with differences. You may learn more about financing from the following articles –

• Calculate Abnormal Return
• Risk Ratio Definition
• Types of Unsystematic Risk
• Types of Risk Factors in Business