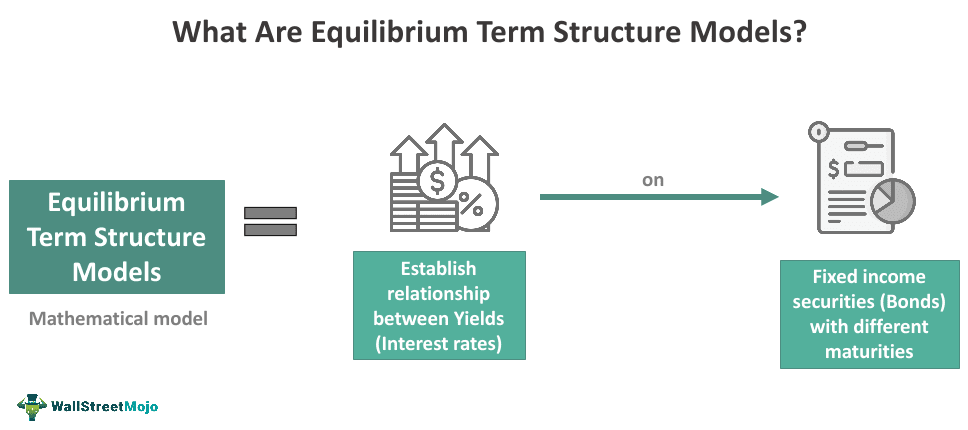
Equilibrium Term Structure Model

The equilibrium term structure models refer to financial/economic models that establish the relationship between interest rates and bond maturity. They aim to determine the most appropriate theoretical interest rate term structures. Further, they are essential in describing, understanding, and identifying mispricing in yield curves.

Many prominent equilibrium models employ macroeconomic variables such as GDP, inflation, unemployment rates, etc. These models can be based on single or multiple variables that affect their utility and accuracy in interest rate predictions and financial analysis. But their objective is the same.

• Equilibrium term structure models are mathematical techniques that analyze the relationship between bond yields and maturity, incorporating macroeconomic assumptions.
• These models provide insights into expected returns from specific bond instruments over different time horizons, such as predicting returns for each year in the next decade.
• Various equilibrium models utilize single or multiple macroeconomic factors, including long-term interest rates, fluctuations, volatility, and other relevant variables.
• Economic analysts, financial experts, advisers, and investors extensively study and employ these models to gain a deeper understanding of bond markets and make informed investment decisions.

Equilibrium term structure models are complex concepts studied by economists, financial analysts, and investors. The idea is essential in the bond market. Let us review a few basic statements before discussing equilibrium models in detail.

The bond market is a predominant focus area for most investors. Bonds are low-risk assets that offer low but assured returns. Yield curves or term structures help market analysts, and traders predict the return (interest rate) from the debt instruments concerning their maturities. The curve varies for different bond instruments at other points in time.

The equilibrium models are techniques that help describe and understand the yield-maturity relationship. For this purpose, these models rely on macroeconomic variables. These models believe that macroeconomic factors such as national income, inflation, national debt, aggregate demand and supply, GDP, unemployment rates, etc., affect the returns from a debt instrument.

Equilibrium models claim that long-term yield rates from a bond depend on short-term interest rates and market expectations and speculations. Here, the financial and economic lens merge. Market expectations affect investors' actions, demand, and supply. They also signal the economy's optimism regarding growth and stability.

It is possible to identify how one macroeconomic variable affects another, which affects others, and the cycle can continue. In this series of influences, many directly and indirectly affect term structure. Equilibrium models seek to establish a precise, discernible relationship between these factors.

Apart from establishing a stochastic relationship, these models also help identify mispricing, risk assessment, market analysis, company or asset's financial analysis, making predictions, and speculating.

A narrow classification of equilibrium models can include one-factor or multi-factor models.

• One-factor models establish the relationship between a single macroeconomic variable and the term structure. This model's demerit is that multiple variables often act on investment returns. Therefore, the situations under consideration need to be more realistic.
• Multi-factor models determine how two or more macroeconomic factors simultaneously or sequentially affect the term structure of interest rates. These models can be more accurate than one-factor models. However, due to multiple variables, the process can get quite complex.

Before going into the broader classification, consider the general stochastic differential equation of interest rates:

dr = m(r, t)dt + s(r, t)dWt

Where,

• dr represents the change in interest rate at time t.
• m(r, t)dt is the drift component. It indicates the average change in interest over time.
• s(r, t) is the diffusion component. It shows the market volatility and fluctuations in interest rates over time.
• dWt is denoted as the change in the Weiner process or Brownian motion. It is a stochastic process and involves the source of randomness.

The broader classification of equilibrium models involves discussing a few prominent models that have already established concrete relationships that explain yield curves. Delving deeper into one-factor models brings us to two other very important models that are widely used in the financial sector. These include the Vasicek Model and the Cox-Ingersoll-Ross Model.

#1 – Vasicek Model

The Vasicek equilibrium model is a one-factor model introduced by Oldrich Vasicek in 1977. The model claims interest rates do not fluctuate widely between extraordinarily high and low values. Instead, it follows the mean reversion theory and returns to its average levels.

The general stochastic differential equation can be extrapolated as:

dr = a (q - r)dt + sdW

Where,

• a is the speed of mean reversion.
• q is the long-term average interest rate.
• An increase or decrease in dr (change in interest rate) will pull back the long-term rates to q at the speed of a.

The main issue with the model is that it can yield negative values mathematically, which is not a realistic situation as it indicates that people will be paying money to the bond issuer instead of receiving returns. Further, it assumes that the volatility is constant.

#2 – Cox-Ingersoll-Ross (CIR) Model

The CIR model is another single-factor model by John Cox, Jonathan Ingersoll, and Stephen Ross in 1985. The model states that the bond yield is a product of a single variable, i.e., market risk. However, the model accounts for volatility, average interest rate, and spreads.

dr =  α (θ - r)dt + σ√rdW

Where,

• α shows the speed of mean reversion.
• θ is the long-term average interest rate.
• The √r term ensures that the interest rate does not become negative.

Moreover, the model assumes that the volatility (s) is directly proportional to changes in interest rates.

Here are a few examples to understand equilibrium term structure models.

Example #1

One factor affecting bond yields is the economic outlook. When the economy performs well and produces more output, the bond yield can be expected to go up. The yield curve will be an upward-sloping one. When the economy underperforms, the curve is inverted.

An investor wants to analyze a particular company's term structure when the economy doesn't perform well but the company's performance booms. He studied the company's bond yields over the past 20 years and compared them to the economy's performance.

The investor found that in periods where the economy didn't perform well but the company did, the bond yield did not show much increase. There was no decrease in yields, but the increase wasn't significant.

Example #2

An equilibrium model states that a yield curve's level, scope, and curvature determine interest rates. It is the Nelson-Seigel model introduced in 1987. The three variables used in the model's logical deduction are the long-term average interest rates, the difference between short-term and long-term rates, and the curvature of the yield curve. It is possible to construct and describe yield curves using observed market data. Further, the model helps in assessing investment risk and making forecasts.

This article has been a guide to What Are Equilibrium Term Structure Model. Here, we explain it in detail along with its types and examples. You may also find some useful articles here -

• Affine Term-Structure Model
• Factor Models
• Spectral Risk Measure