Population Mean Formula

The population means is the mean or average of all values in the given population. It is calculated by the sum of all values in the population, denoted by the summation of X divided by the number of population values denoted by N.

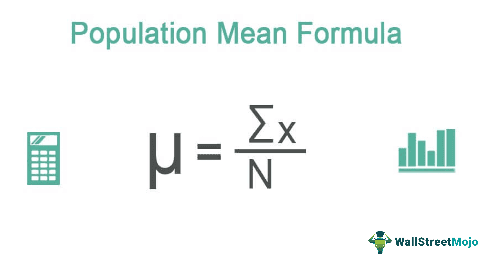
It arrives by summing up all the observations in the group and dividing the summation by the number of observations. When one uses the whole data set for computing a statistical parameter, the data set is the population. For example, the returns of all the stocks listed in the NASDAQ stock exchange in the population of that group. So, for this example, the population means that the return of all the stocks listed in the NASDAQ stock exchange will be the average return of all the stocks listed in that exchange.

The population mean formula is used in the field of statistics to represent and measure the average value of a variable in an entire set of population. It is calculated as the summation of all the individual variables in the population divided by the total number of all the variables.

To calculate the population mean for a group, we need to use the formula for population mean. At first we need to find out the sum of all the observed values. So, if the total number of observed values is denoted by X, then the summation of all the observed values will be ∑X. And let the number of observations in the population be N.

The formula is represented as follows,

µ= ∑X/N

• µ= Population mean

The resultant value obtained from the calculation represents the average of the entire population.

This method is often used in situation where it is not possible to calculate or count the entire population in order to draw any conclusion. This is mainly due to the size constraint. In such cases some samples are taken from the entire population which is used as an estimate or representation. This is a widely used method in the field of statistics.

Let us try to understand the concept of need to use the formula for population mean with the help of some suitable examples as given below:

Example #1

Let us analyze the return of a stock XYZ for the last twelve years. And the returns for the stock in the last twelve years are 12%, 25%, 16%, 14%, 40%, 15%, 13%, 17%, 23%, 13%, 17%, and 19%. To calculate the mean for the whole population, we must first find out the summation of all the observed values. So in this example, the ∑X is 224%, and the number of observed values for the population is 12 as it comprises the return for the stock for 12 years period.

With these two variables, we can calculate the population mean for the stock return with the formula's help of formula for population mean.

The following is the given data:

Therefore, using the above information mean can be calculated as,

• µ= 224%/12

The example shows that the mean or average return for the observed value is 19% which we calculate with the help of population mean formula statistics. 

Example #2

Let us analyze the return of a thematic mutual fund for the last eight years. And the returns for the stock in the last twelve years are 25%, 16%, 14%, 15%, 13%, 23%, 33%, and 27%. To calculate the mean for the whole population, we must first find the summation of all the observed values. So in this example, the ∑X is 166%, and the number of observed values for the population is 8 as it comprises the return of the mutual fund for 8 years.

With these two variables, we can calculate the population mean for the stock return with the formula's help.

Below is given data for the calculation:

Therefore, the mean can be calculated using the population mean formula statistics as,

• µ= 166%/8

The example shows that the mean or average return for the observed value is 21%. 

Example #3

Let us find out the population mean of the weight of 15 students in a class. The weight of each student in the class of 15 students in kg is as follows 35, 36, 42, 40, 44, 45, 38, 42, 39, 42, 44, 45, 48, 42, and 40. To calculate the mean for the whole population, we must first find out the summation of all the observed values. So in this example, for the purpose of estimating population mean formula, we see that the ∑X is 622 Kg, and the number of observed values for the population is 15 as it comprises the weight of 15 students.

With these two variables, we can calculate the population mean for the stock return with the formula's help.

The following are the given data for the calculation:

Therefore, using the above information population average can be calculated using the sample population mean formula as,

• µ= 622/15

 The example shows that the mean or average return for the observed value is 41.47.

The above examples clearly explain the concept of estimating population mean formula in detail and also point out some situations where it can be used successfully and how the formula helps find the required information.

The population means is a very important statistical parameter. It helps in knowing the average of the population's parameters. The sample population mean formula is important as one can use it to calculate several other statistical parameters like the variance, standard deviations, and others. One may calculate it using the concept of the arithmetic mean formula. It represents the average or means based on which one can infer whether an observation is high or low in the whole population of observations.