Table Of Contents
What Is The Quartile Formula?
The quartile formula is a statistical tool to calculate the variance from the given data by dividing the same into four defined intervals, comparing the results with the entire set of observations, and commenting on the differences in the data sets.

The quartile formula is often used in statistics to measure the variances, which describe a division of all the given observations into four defined intervals based on the data values and where they stand when compared with the entire set of the given observations.
Key Takeaways
- A quartile formula is a statistical tool that calculates the variance from the provided data by dividing the same into four defined intervals,
- comparing the results with the whole observations, and commenting on the differences in the data sets.
- One may use it in statistics to calculate the variances that separate all the given observations into four defined intervals.
- It is divided into 3 points: a lower quartile, indicated by Q1, comes between the smallest value and the median of the provided data set.
- The median, denoted by Q2, is the median, and the upper quartile, indicated by Q3, is the middle point.
Quartile Formula Explained
Quartile formula, as the name suggests segments an observation or dataset into different quarters. The statisticians or users draw a median that divides the data into two parts and then the quartile divides it further.
This way, the quartile formula divides into 3 points: a lower quartile formula, denoted by Q1, which falls between the smallest value and the median of the given data set. The median quartile formula, denoted by Q2, is the median, and the upper quartile formula, denoted by Q3, is the middle point between the median and the highest number of the given distribution dataset.
The Quartile Formula in statistics for respective quarters is represented as follows:
The Quartile Formula for Q1= ¼(n+1)th term The Quartile Formula for Q3= ¾(n+1)th term The Quartile Formula for Q2= Q3–Q1(Equivalent to Median)
The quartiles will divide the measurements of the given data set or sample into four similar or equal parts. For example, 25% of the given dataset's measurements (represented by Q1) are not greater than the lower quartile. 50% of the measurements are not greater than the median, i.e., Q2; lastly, 75% will be less than the upper quartile that Q3 denotes. Therefore, 50% of the measurements of the given dataset are in between Q1, the lower quartile, and Q2, the upper quartile.
Examples
Let us see some simple to advanced examples of a quartile in excel to understand it better.
Example #1
Consider a data set of the following numbers: 10, 2, 4, 7, 8, 5, 11, 3, 12. You are required to calculate all the 3 quartiles.
Solution:
Use the following data for the calculation of quartile.
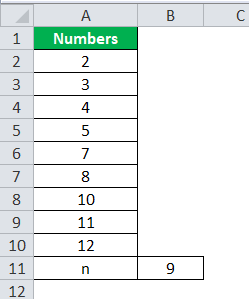
Calculation of Median or Q2 can be done as follows,
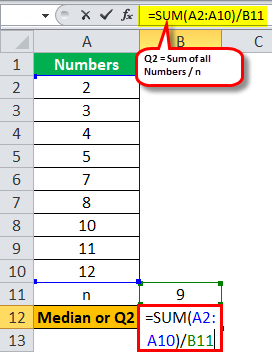
Median or Q2 = Sum(2+3+4+5+7+8+10+11+12)/9
Median or Q2 will be -

Median or Q2 = 7
Since the number of observations is odd, which is 9, the median would lie in the 5th position, which is 7, and the same will be Q2 for this example.
Calculation of Q1 can be done as follows,
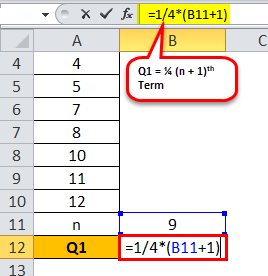
Q1= ¼ (9 + 1)
= ¼ (10)
Q1 will be -
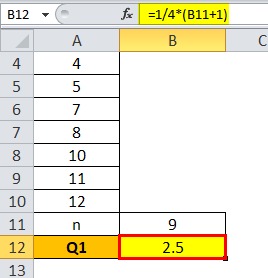
Q1 = 2.5
This means that Q1 is the average of 2nd and 3rd position of the observations, which is 3 & 4 here, and the average of the same is (3+4)/2 = 3.5
Calculation of Q3 can be done as follows,
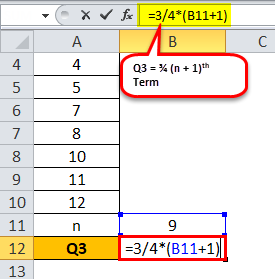
Q3 = ¾ (9 + 1)
= ¾ (10)
Q3 will be -
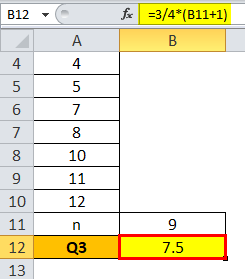
Q3 = 7.5 Term
It means that Q3 is the average of the 8th and 9th positions of the observations, which is 10 and 11 here. So the same average is (10+11)/2 = 10.5.
Example #2
Simple Ltd. is a clothing manufacturer working on a scheme to please their employees for their efforts. The management is in discussion to start a new initiative which states they want to divide their employees as per the following:
- Top 25% lying above Q3- $25 per cloth
- Greater than the middle one but less than Q3 – $20 per cloth
- Greater than Q1 but less than Q2 – $18 per cloth
- The management has collected its average daily production data for the last 10 days per (average) employee.
- 55, 69, 88, 50, 77, 45, 40, 90, 75, 56.
- Use the quartile formula to build the reward structure.
- What rewards would an employee get if he produced 76 clothes ready?
Solution:
Use the following data for the calculation of quartile.
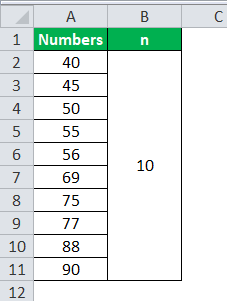
40, 45, 50, 55, 56, 69, 75, 77, 88, 90
The calculation of quartile Q1 can be as follows:

Q1 = ¼ (n+1)th term
= ¼ (10+1)
= ¼ (11)
Q1 will be -
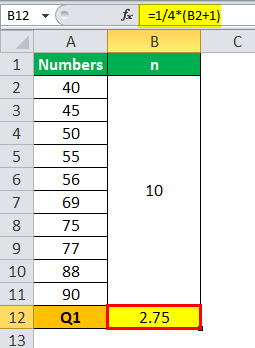
Q1 = 2.75 Term
Here, the average must be taken, which is of 2nd and 3rd terms, which are 45 and 50. The average formula of the same is (45+50)/2 = 47.50
The Q1 is 47.50, which is bottom 25%
Calculation of quartile Q3 can be done as follows,
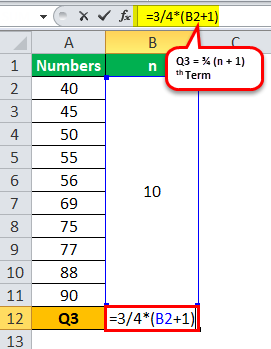
Q3 = ¾ (n+1)th term
= ¾ (11)
Q3 will be -
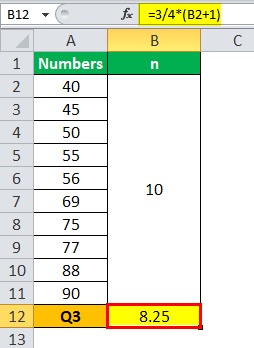
Q3 = 8.25 Term
Here, the average needs to be taken, which is of 8th and 9th terms, which are 88 and 90. The average of the same is (88+90)/2 = 89.00.
The Q3 is 89, which is the top 25%.
The calculation of the median or Q2 can be as follows:
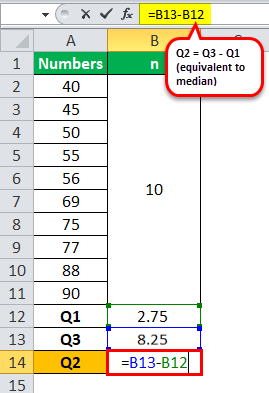
The Median Value (Q2) = 8.25 - 2.75
Median or Q2 will be -
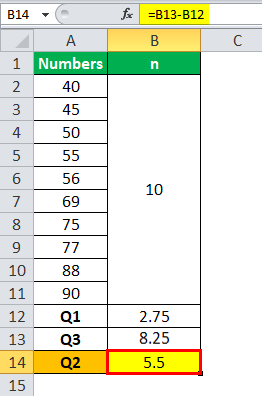
Median or Q2= 5.5 Term
Here, the average needs to be taken, which is of 5th and 6th 56 and 69. The average of the same is (56+69)/2 = 62.5.
The Q2 or median is 62.5
Which is 50% of the population.
The Reward Range would be:
47.50 – 62.50 will get $18 per cloth
>62.50 – 89 will get $20 per cloth
>89.00 will get $25 per cloth
If an employee produces 76, he will lie above Q1. Hence, would be eligible for a $20 bonus.
Example #3
Teaching private coaching classes is considering rewarding students in the top 25% quartile advice to interquartile students lying in that range and retake sessions for the students lying below Q1.Use the quartile formula to determine what repercussions he will face if he scores an average of 63.
Solution :
Use the following data for the calculation of quartile.
The data is for the 25 students.
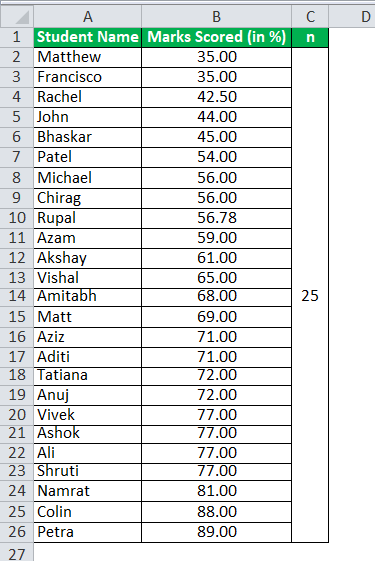
The calculation of quartile Q1 can be as follows:
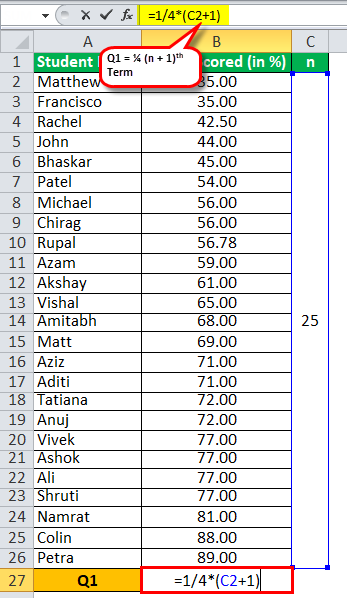
Q1 = ¼ (n+1)th term
= ¼ (25+1)
= ¼ (26)
Q1 will be -
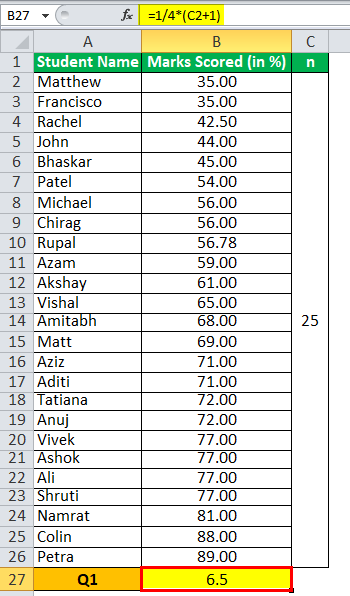
Q1 = 6.5 Term
The Q1 is 56.00, which is the bottom 25%
Calculation of quartile Q3 can be done as follows,
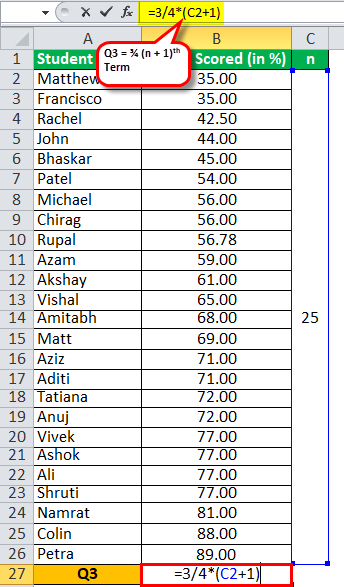
Q3 = ¾ (n+1)th term
= ¾ (26)
Q3 will be -
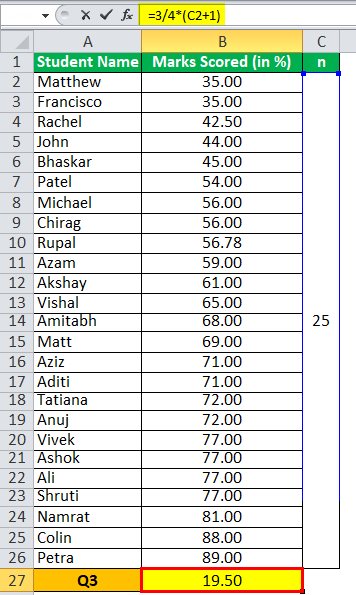
Q3 = 19.50 Term
Here, the average needs to be taken, which is of 19th and 20th terms, which are 77 and 77. The average of the same is (77+77)/2 = 77.00.
The Q3 is 77, which is the top 25%.
Median or Q2 will be –
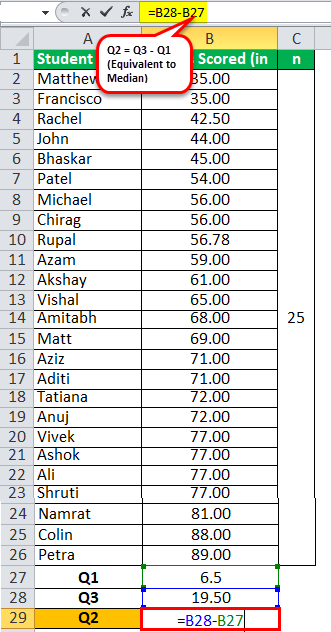
Median or Q2=19.50 - 6.5
Median or Q2 will be -
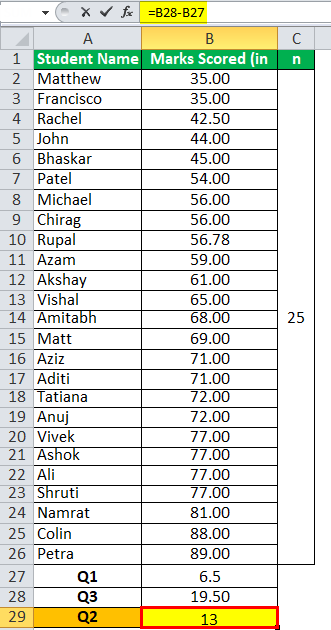
Median or Q2 = 13 Term
The Q2 or median is 68.00
Which is 50% of the population.
The Range would be:
56.00 – 68.00
>68.00 – 77.00
77.00
Relevance and Use
Quartile formula helps in grouping data appropriately, thereby helping users identify and evaluate the datasets as required.
Listed below are the points that mention the relevance and uses of this equation:
- Quartiles let one quickly divide a given dataset or sample into four major groups, making it easy for the user to evaluate which of the four groups a data point is.
- While the median, which measures the central point of the dataset, is a robust estimator of the location. It does not say how much the data of the observations lie on either side or is dispersed or spread.
- The quartile measures the spread or dispersion of values above and below the arithmetic mean or average, dividing the distribution into four major groups discussed above.

