Standard Error Formula

What is a Standard Error Formula?

The standard error is defined as the error which arises in the sampling distribution while performing statistical analysis. This is basically a variant of standard deviation as both concepts correspond to the spread measures. A high standard error corresponds to the higher spreading of data for the undertaken sample. Calculation of the standard error formula is done for a sample, whereas the standard deviation is determined for the population.

Therefore, a standard error on mean would be expressed and determined as per the relationship described as follows: –

Here,

• The standard error is expressed as σ_͞x.
• The standard deviation of the population is expressed as σ.
• The number of variables in the sample is expressed as n.

In statistical analysis, mean, median, and mode are considered as the central tendency measures. Whereas the standard deviation, variance, and standard error on mean are classified as the variability measures. The standard error on mean for sample data is directly related to the standard deviation of the larger population and inversely proportional or related to the square root of a number of variables taken up for making a sample. Hence if the sample size is small, then there could be an equal probability that the standard error would also be large.

Explanation

The formula for standard error on mean can be explained by using the following steps:

• Step 1: Firstly, identify and organize the sample and determine the number of variables.
• Step 2: Next, the average means of the sample corresponding to the number of variables present in the sample.
• Step 3: Next, determine the standard deviation of the sample.
• Step 4: Next, determine the square root of the number of variables taken up in the sample.
• Step 5: Now, divide the standard deviation computed in step 3 with the resulting value in step 4 to arrive at the standard error.

Example of Standard error formula

Given below are the formula examples for the calculation of standard error.

Example #1

Let us take the example of stock ABC. For the tenure of 30 years, the stock delivered a mean dollar return of $45. It was observed that the stock delivered the returns with a standard deviation of $2. Help the investor to calculate the overall standard error on the mean returns offered by the stock ABC.

Solution:

Calculation of standard error is as follows –

• σ_͞x = σ/√n
• = $2/√30
• = $2/ 5.4773

Standard Error is,

• σ_͞x =$0.3651

Therefore, the investment offers a dollar standard error on the mean of $0.36515 to the investor when held the position in the stock ABC for 30 years. However, if the stock is held for a higher investment horizon, then the standard error on the dollar means would reduce significantly.

Example #2

Let us take the example of an investor who has received the following returns on stock XYZ: –

Help the investor for the calculation of overall standard error on the mean returns offered by the stock XYZ.

Solution:

First determine the average mean of the returns as displayed below: –

• ͞X = (x1+x2+x3+x4)/number of years
• = (20+25+5+10)/4
• =15%

Now determine the standard deviation of the returns as displayed below: –

• σ = √ ((x1-͞X)² + (x2-͞X)² + (x3-͞X)² + (x4-͞X)²) / √ (number of years -1)
• = √ ((20-15) ² + (25-15) ² + (5-15) ² + (10-15) ²) / √ (4-1)
• = (√ (5) ² + (10) ² + (-10) ² + (-5) ² ) / √ (3)
• = (√25+100+100+25)/ √ (3)
• =√250 /√ 3
• =√83.3333
• = 9.1287%

Now the calculation of standard error is as follows,

• σ_͞x = σ/√n
• = 9.128709/√4
• = 9.128709/ 2

Standard Error is,

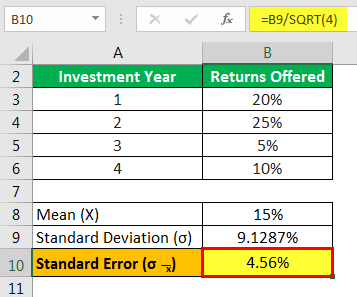
• σ_͞x = 4.56%

Therefore, the investment offers dollar standard error on the mean of 4.56% to the investor when held the position in the stock XYZ for 4 years.

Standard Error Calculator

You can use the following calculator.

Relevance and Use

The standard error tends to be high if the sample size taken up for the analysis is small. A sample is always taken up from a larger population, which comprises a larger size of variables. It always helps the statistician to determine the credibility of the sample mean with respect to the population mean.

A large standard error tells the statistician that the sample is not uniform with respect to the population mean, and there is the presence of large variation in the sample with respect to the population. Similarly, a small standard error tells the statistician that the sample is uniform with respect to the population mean, and there is the presence of no or small variation in the sample with respect to the population.

It should not be mixed with the standard deviation. The standard deviation is calculated for the entire population. The standard error, on the other hand, is determined for the sample mean.

Standard Error Formula in Excel

Now, let us take the excel example to illustrate the concept of standard error formula in the excel template below. Suppose the administration of the school wants to determine the standard error on mean on the height of the football players.

The sample comprises of following values: –

Help the administration assess standard error on mean.

Step 1: Determine the mean as displayed below: –

Step 2: Determine the standard deviation as displayed below: –

Step 3: Determine the standard error on mean as displayed below: –

Therefore, the standard error on mean for the football players is at 1.846 inches. The management should observe that it is significantly large. Therefore, the sample data taken up for the analysis is not uniform and displays a large variance.

The management should either omit out smaller players or add players to are significantly taller to balance the football team average height by replacing them with individuals who have smaller heights as compared with their peers.

Recommended Articles

This has been a guide to Standard Error Formula. Here we discuss the formula for the calculation of standard error of mean along with the examples and downloadable excel sheet. You can learn more from the following articles –

• EBITDA Margin Formula
• Gross Margin Formula
• Formula of Relative Standard Deviation
• Formula of Margin of Error