Quartile Deviation

Quartile deviation depends on the difference between the first quartile and the third quartile in the frequency distribution. The difference is also known as the interquartile range. The difference divided by two is known as quartile deviation or semi-interquartile range.

When one takes half of the difference or variance between the 3rd quartile and the 1st quartile of a simple distribution or frequency distribution is the quartile deviation.

• Quartile deviation is the difference in the frequency distribution between the first and third quartiles. Therefore, it is also called the interquartile range. Moreover, If the difference is divided by two, it is known as quartile deviation or semi-interquartile range.
• One may use the Quartile Deviation (Q.D.) statistical formula to measure spread or dispersion, called a semi-interquartile range.
• The quartile deviation or semi-interquartile range is used to learn or say a study about the dispersion of the observations or the samples of the given data sets in the given series main or middle body.

A Quartile Deviation (Q.D.) formula is used in statistics to measure spread or, in other words, to measure dispersion. It can also be called a semi-interquartile range.

• The formula includes Q3 and Q1 in the calculation, which is the top 25% and lower 25% data, respectively. When the difference is between these two, and this number halves, it gives measures of spread or dispersion.
• So, to calculate quartile deviation, you need first to find out Q1, then the second step is to find Q3 and then make a difference between both, and the final step is to divide by 2.
• It is one of the best methods of dispersion for open-ended data.

Example #1

Consider a data set of following numbers: 22, 12, 14, 7, 18, 16, 11, 15, 12. You are required to calculate the Quartile Deviation.

Solution:

First, we need to arrange data in ascending order to find Q3 and Q1 and avoid any duplicates.

7, 11, 12, 13, 14, 15, 16, 18, 22

Calculation of Q1 can be done as follows,

Q1 = ¼ (9 + 1)

=¼ (10)

Q1=2.5 Term

Calculation of Q3 can be done as follows,

Q3=¾ (9 + 1)

=¾ (10)

Q3= 7.5 Term

Calculation of quartile deviation can be done as follows,

• Q1 is an average of 2nd, which is 11, and adds the difference between 3rd & 4th and 0.5, which is (12-11)*0.5 = 11.50.
• Q3 is the 7th term and the product of 0.5. The difference between the 8th and 7th terms is (18-16)*0.5, and the result is 16 + 1 = 17.

Q.D. = Q3 - Q1 / 2

Using the quartile deviation formula, we have (17-11.50) / 2

=5.5/2

Q.D.=2.75.

Example #2

Harry Ltd. is a textile manufacturer and is working on a reward structure. The management is discussing starting a new initiative, but they first want to know how much their production spread is.

The management has collected its average daily production data for the last ten days per (average) employee.

155, 169, 188, 150, 177, 145, 140, 190, 175, 156.

Use the Quartile Deviation formula to help management find dispersion.

Solution:

The number of observations here is 10, and our first step would be to arrange data n ascending order.

140, 145, 150, 155, 156, 169, 175, 177, 188, 190

Calculation of Q1 can be done as follows,

Q1= ¼ (n+1)th term

=¼ (10+1)

=¼ (11)

Q1= 2.75^th Term

Calculation of Q3 can be done as follows,

Q3= ¾ (n+1)th term

=¾ (11)

Q3= 8.25 Term

Calculation of quartile deviation can be done as follows,

• 2^nd term is 145 and now adding to this 0.75 * (150 – 145) which is 3.75, and the result is 148.75
• 8^th term is 177 and now adding to this 0.25 * (188 – 177) which is 2.75, and the result is 179.75

Q.D. = Q3 - Q1 / 2

Using the quartile deviation formula, we have (179.75-148.75) / 2

=31/2

Q.D.=15.50.

Example #3

Ryan’s International Academy wants to analyze how many percentage scores marks their students spread out.

The data is for the 25 students.

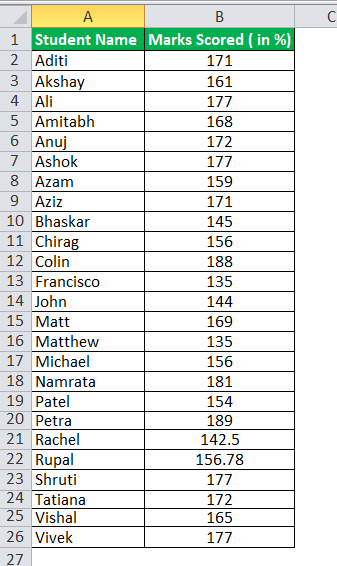
Use the Quartile Deviation formula to find out the dispersion in % marks.

Solution:

The number of observations here is 25. So, our first step would be to arrange data in ascending order.

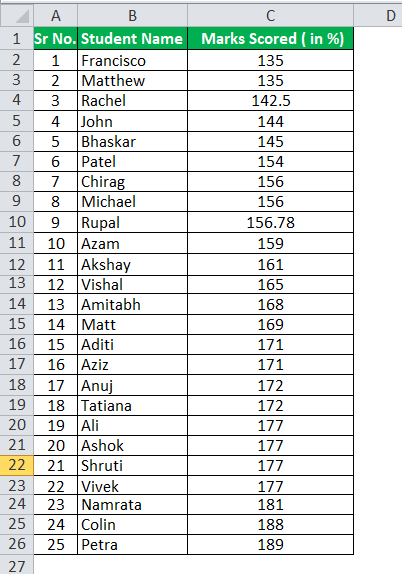
Calculation of Q1 can be done as follows,

Q1= ¼ (n+1)th term

=¼ (25+1)

=¼ (26)

Q1= 6.5^th Term

Calculation of Q3 can be done as follows,

Q3=¾ (n+1)th term

=¾ (26)

Q3 = 19.50 Term

Calculation of quartile deviation or semi interquartile range can be done as follows,

• 6^th term is 154 and now adding to this 0.50 * (156 – 154) which is 1, and the result is 155.00
• 19^th term is 177 and now adding to this 0.50 * (177 – 177) which is 0, and the result is 177

Q.D. = Q3 - Q1 / 2

Using the quartile deviation formula, we have (177-155) / 2

=22/2

Q.D.= 11.

Example #4

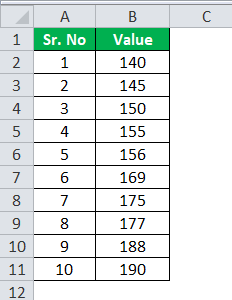
Let us now determine the value through an excel template for Practical example I.

Solution:

Use the following data for the calculation of quartile deviation.

Calculation of Q1 can be done as follows,

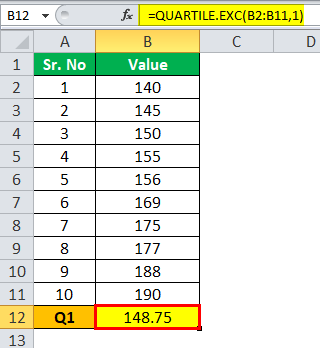
Q1=148.75

Calculation of Q3 can be done as follows,

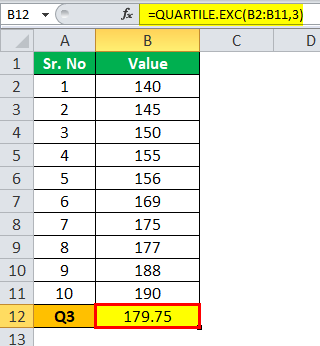
Q3= 179.75

Calculation of quartile deviation can be done as follows,

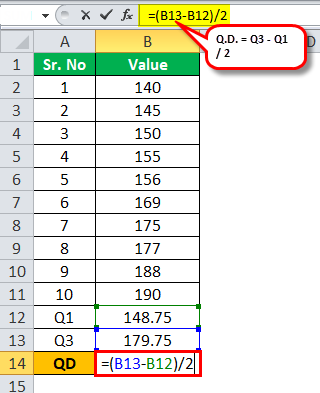
Using the quartile deviation formula, we have (179.75-148.75 )/ 2

Q.D. will be -

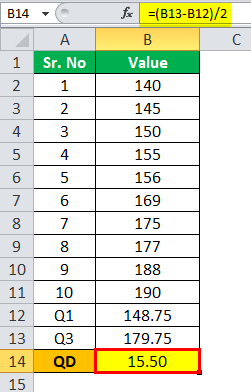
QD = 15.50

Quartile deviation is also known as a semi-interquartile range. Again, the difference in the variance between the 3rd and 1st quartiles is known as the interquartile range. The interquartile range depicts the extent to which the observations or the values of the given dataset spreads out from the mean or their average. The quartile deviation or semi-interquartile range is the majority used in a case where one wants to learn or say a study about the dispersion of the observations or the samples of the given data sets that lie in the main or middle body of the given series. This case would usually happen in a distribution where the data or the observations tend to lie intensely in the main body or middle of the given data set or the series. The distribution or the values do not lie towards the extremes. If they lie, then they are not of much significance for the calculation.

This article has been a guide to Quartile Deviation Formula. Here, we discuss calculating quartile deviation in Excel with practical examples and a downloadable Excel template. You can learn more about Excel modeling from the following articles: -

• Formula of Quartile 
• Portfolio Standard Deviation
• Calculate Relative Standard Deviation
• Decile
• Point Estimators