Geometric Mean

Publication Date :

06 Feb, 2022

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Geometric Mean Definition

Geometric Mean (GM) is a central tendency method that determines the power average of a growth series data. It is computed as the n^th root of the multiplicative result of all the data figures up to n.

The method is suitable for determining the average value appreciation of a particular investment or the overall portfolio—for a given time frame. It accurately evaluates average values pertaining to a continuous series of interdependent values.

Key Takeaways

The geometric mean (GM) refers to a central tendency measure that evaluates the average of a series by multiplying all the numbers and then finding the nth root of the product.
It is the power mean used for a continuous data series with a close-end distribution of the interdependent values or items.
The GM method is applied to compute the proportional growth of stock indices. Further, it ascertains the average returns of investments or portfolios that provide compounding benefits.

Geometric Mean Explained

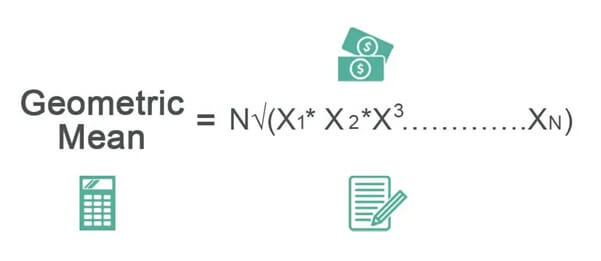
The geometric mean is used with time-series data to ascertain the compounding average. Time series data is a culmination of observations collected through repeated measurements over time. When time-series data is represented on a graph, one of the axes would always be time.

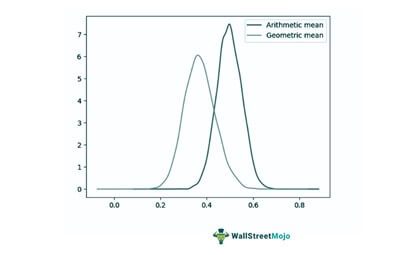
Geometric Mean Graph 1 — *You are free to use this image on your website, templates, etc..* *Please provide us with an attribution link.*

This metric is often referred to as power mean. It is mostly used to compare the growth averages of different investment products or portfolios. It has an exponential relationship with the arithmetic mean of logarithms.

This method normalizes ranges, reducing the impact of dominant values on the weightage. Thus, enormous values no longer influence skewed distribution patterns. This method provides better results when variables are widely skewed.

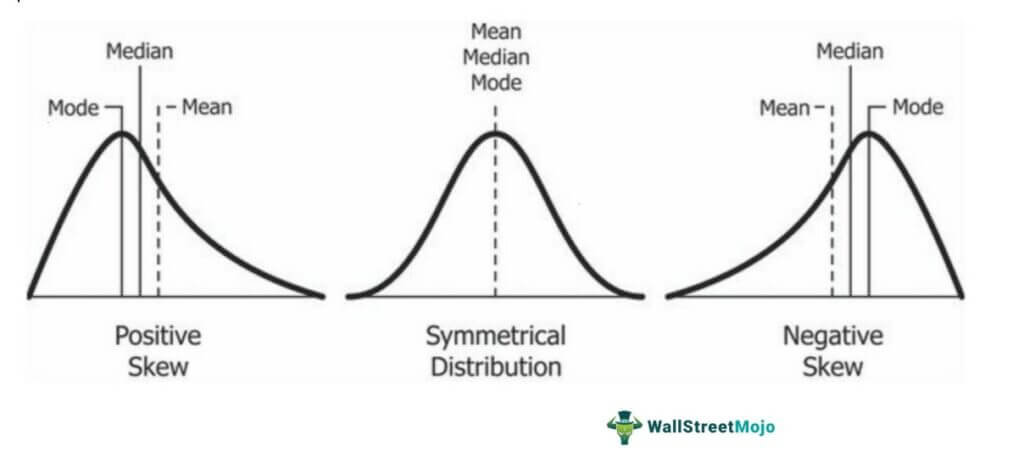
Graph 1-1 — *You are free to use this image on your website, templates, etc..* *Please provide us with an attribution link.*

Skewness refers to symmetry. If skewness is 0, the data is perfectly symmetrical. If the normal distribution is uneven with a skewness greater than zero or positive skewness, then its right tail will be more prolonged than the left.

Properties

The following properties make geometric mean stand out among other central tendency measures:

Even if each value in the data series is replaced with the GM, their product will still be the same.
In a particular data set, the geometric mean value is always lower than the value of its arithmetic mean.
When the corresponding observations of GM of two data series are multiplied, the value acquired is equal to the multiplicative result of their GM values.

Geometric Mean Formula

The geometric mean calculation helps investors ascertain the compounding average for a given data series. It is evaluated using the following formulas:

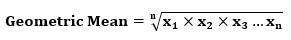
Or,

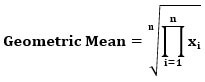
In the above equations, n is the total number of values in a given data series. Also, x₁, x_2,andx₃are the provided data series's first, second, and third values. In addition, x_n is the n^th value of the provided data series.

Geometric Mean Calculation

Given below are the basic steps of Geometric Mean calculation:

Make sure that the provided data series has interdependent and progressive values.
Count the number of values or items in the series to determine “n.”
Now, multiply all the values in the given sequence.
Then, find the n^th root of the product acquired in the previous step to obtain GM.

Example

Rhonda is a soccer player. In a five-month selection process for the interstate competition, she scored 3,7, 8, 11, and 17 goals respectively. Determine the geometric mean to analyze her overall performance.

Solution:

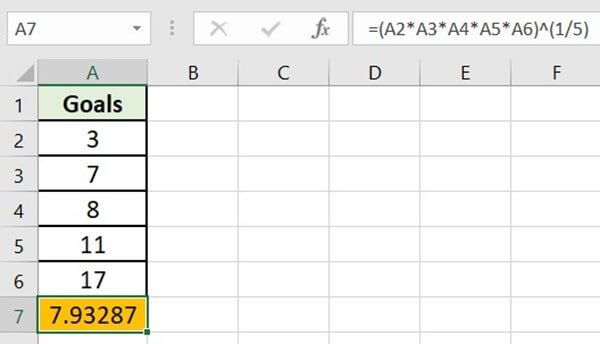
Note: In the above sheet, we have applied the formula ⁿ√ (x₁*x₂* x₃…x_n) or (x₁*x₂* x₃…x_n) ^(1/n).

Hence, on average, Rhonda scores 7.93 or 8 goals.

Application

Geometric Mean is a reliable method for determining the average rate of return of an investment or the investment portfolio—for a given year. It facilitates the comparison of the two or more investment opportunities or assets and helps select the better option.

It is used to determine the average compounded growth rate of stocks and other securities. Further, it is applied on stock indices that hold stocks of equivalent weightage—varying in market capitalization.

In geometry, the geometric mean is applied to exponential values. GM is also applied in biology to research bacterial growth, viral mutation rates, and cell division. Economists employ this method for understanding population growth and average voter turnouts.

Advantages and Disadvantages

The geometric mean is beneficial for identifying the average of rigid sequences. However, unlike the arithmetic mean, a higher level of weightage is vested upon small values. Moreover, sampling fluctuations have little impact on GM results.

The method sure has limitations, the foremost being its complexity. As a result, it is less popular. Users require thorough mathematical knowledge of ratios, roots, and logarithms—application is difficult for a layman.

The method is not a suitable measure for data series with zero or negative values. Similarly, the method cannot be applied to data series with open-end distributions.