Sample Mean vs Population Mean

Publication Date :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

arrow

Difference between Sample Mean vs Population Mean

In statistics, there are two different averages: the sample mean and the population mean. The sample mean only considers a selected number of observations—drawn from the population data. The population mean, on the other hand, considers all the observations in the population—to compute the average value.

Sample vs Population Mean

The method of mean computation is the same in both cases. But, when the population size is large, a sample mean is determined to get an approximate value that represents the entire population. Computing the sample mean is easy, whereas computation of the population mean a tedious process.

Table of contents

Comparative Table

Sample Mean Vs Population Mean Differences are as follows:

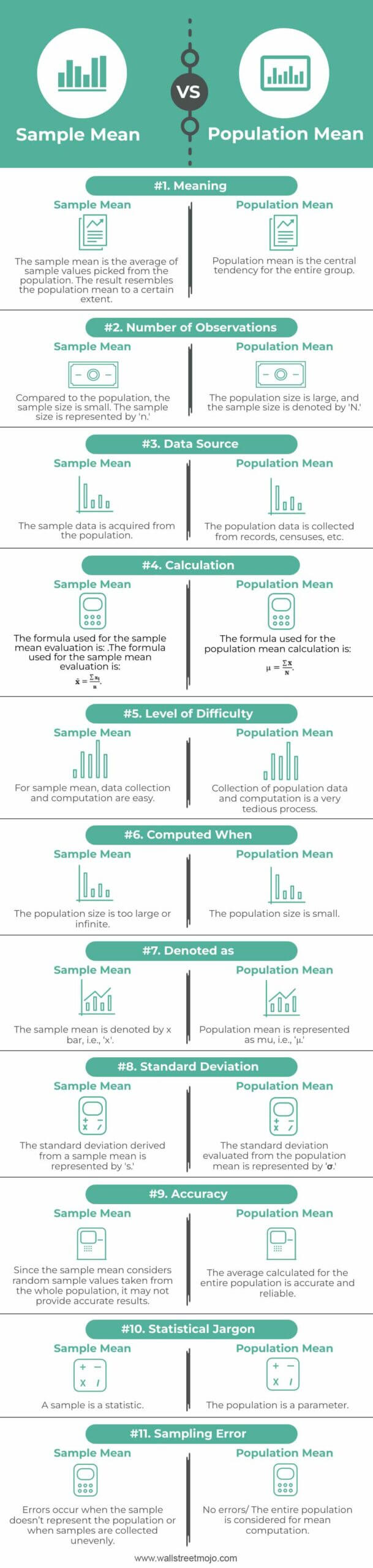
BasisSample MeanPopulation Mean
MeaningThe sample mean is the average of sample values picked from the population. The result resembles the population mean to a certain extent.Population mean is the central tendency for the entire group.
Number of ObservationsCompared to the population, the sample size is small. The sample size is represented by 'n.'The population size is large, and the sample size is denoted by 'N.'
Data SourceThe sample data is acquired from the population.The population data is collected from records, censuses, etc.
CalculationThe formula used for the sample mean evaluation is: x̄ =∑xi /nThe formula used for the population mean calculation is: μ=∑X / N
Level of DifficultyFor sample mean, data collection and computation are easy.The collection of population data and computation is a very tedious process.
Computed WhenThe population size is too large or infiniteThe population size is small
Denoted asThe sample mean is denoted by x bar, i.e., 'x̄'.Population mean is represented as mu, i.e., 'μ'.
Standard DeviationThe standard deviation derived from a sample mean is represented by 's.'The standard deviation evaluated from the population mean is represented by 'σ'.
AccuracySince the sample mean considers random sample values taken from the whole population, it may not provide accurate results.The average calculated for the entire population is accurate and reliable.
Statistical JargonA sample is a statistic.The population is a parameter.
Sampling ErrorErrors occur when the sample doesn’t represent the population or when samples are collected unevenly.No errors—the entire population is considered for mean computation.

What is Sample Mean?

The sample mean is a central tendency measure. The arithmetic average is computed using samples or random values taken from the population. It is evaluated as the sum of all the sample variables divided by the total number of variables.

It is computed using the following formula:

x̄ =∑xi /n

  • Here, x̄ is the sample mean.
  • ∑xi is the sum of all the sample observations.
  • n is the sample size or the total number of observations.

The simple random sampling method is considered unbiased and reliable for determining the sample mean. Simple random sampling is a process where each article or object in the population has an equal chance of getting selected. Thus, It closely represents the result an analyst would have received upon computing the average of the entire population.

Sampling may not always provide the correct result. If a sample represents the population unevenly, it is referred to as a sampling error.

Sample Mean Example

Let us look at an example to understand sample mean calculations:

A preschool authority wants to know the approximate average weight of students. Out of 360 students, 40 students are randomly selected for weighing:

Number of StudentsWeight (Kg)Number of Students × Weight (Kg)
21428
314.543.5
11515
115.515.5
31648
216.533
41768
317.552.5
21836
518.592.5
11919
419.578
32060
120.520.5
521105
40-714.5

Clearly, ∑xi = 714.5 Kgs

And, n = 40

Now let us apply the values to the formula:

x̄ =∑xi /n

x̄ = 714.5 / 40 = 17.86 Kgs

Hence, the approximate average weight of preschool students is 17.86 kgs.

What is Population Mean?

A population mean is the average computed from the entire group, distribution, or population. It is derived by dividing the aggregate of all the population variables by the total number of variables in the population.

Population-Mean-Formula

Population Mean is denoted by the following formula:

μ=∑X / N

  • Here, μ is the population mean.
  • ∑X is the sum of all the observations in the population.
  • N is the population size or the number of total variables in the data set.

When the population size is too large for computation or has an infinite or uncountable number of observations, a sample mean is calculated. This is undertaken using the random sampling method. Also, the sample mean is believed to closely interpret the result of the population mean—if there are no sampling errors.

Population Mean Example

Let us assume that the prices of ABC stock at the end of every trading day for 20 days of a month are as follows:

$15.15, $15.42, $14.91, $14.78, $15.12, $15.56, $15.36, $15.13, $15.31, $14.79, $15.11, $15.31, $15.27, $14.49, $14.77, $14.35, $14.64, $15.21, $15.38, and $15.44.

Now, based on the given data, determine the population mean.

Solution:
μ=∑X / N

μ = ($15.15 + $15.42 + $14.91 + $14.78, $15.12 + $15.56, $15.36 + $15.13 + $15.31 + $14.79 + $15.11 + $15.31 + $15.27 + $14.49 + $14.77 + $14.35 + $14.64 + $15.21 + $15.38 + $15.44) / 20 = 301.5 / 20 = $15.07

Thus, the population mean of ABC stock prices is $15.07.

Sample Mean Vs Population Mean Infographics

Let us look at Sample Mean Vs Population Mean infographics to understand the differences between the two averages better.

Sample-Mean-vs-Population-Mean-info

Similarities

Sample Mean Vs Population Mean similarities are as follows:

Both are types of the arithmetic mean. Arithmetic mean is a statistical tool that determines the central tendency of a given set of data. Also, the computation methods for both the means are the same. For computing, the sum of all the observations in a given data set is divided by the total number of observations.

Conclusion

  • The sample mean is the central tendency acquired from the sample data. The sample data is drawn from the population. Statistically, the sample mean is represented by 'x̄.'
  • On the contrary, the population mean is the average value of all the observations in a given population or group. It is represented by 'μ.'
  • The sample mean sometimes lacks accuracy due to sampling errors and may not fairly depict the population mean. Even so, it is not always possible to determine the population mean when the population size is too large.