Arithmetic Mean

What is Arithmetic Mean?

Arithmetic Mean, commonly used term in statistics, is the average of the numerical values set and is calculated by firstly calculating the sum of number in the set and then dividing resultant by count of those numbers.

Arithmetic Mean Formula

The formula is represented as below :

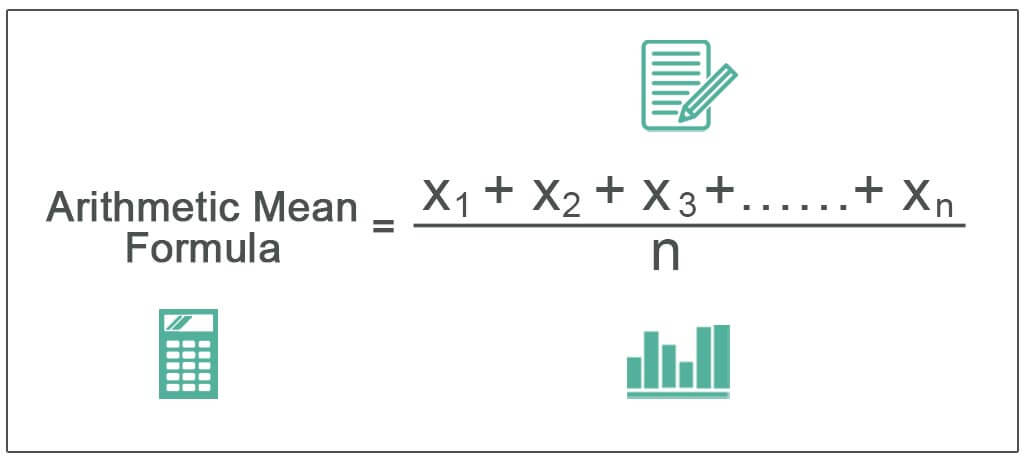
Where,

• x_1, x_2, x_3, x_n are the observations
• n is the number of observations

Alternatively, it can be symbolically written as shown below-

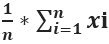
In the above Equation, the symbol  ∑ is known as sigma. It implies the summation of the values.

Steps to Calculate Arithmetic Mean

• Step 1: Calculate the sum of all the observations.

• • x₁ + x₂ + x₃ +…….+ x_n
• Step 2: Determine the number of observations. The number of observations is denoted by n.
• Step 3: Calculate the arithmetic mean using:

• • Arithmetic Mean = x1+x2+x3+…………….+xn/n
  • Alternatively, Arithmetic Mean Formula in symbolic terms is represented as below,

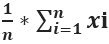
Examples

Example #1

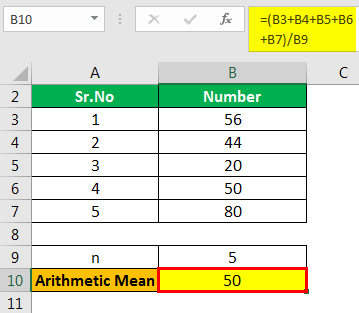
There are five observations. These are 56, 44, 20, 50, 80. Find their arithmetic mean.

Solution

• Here, the observations are 56, 44, 20, 50, 80.
• n = 5

Therefore, the calculation is as follows,

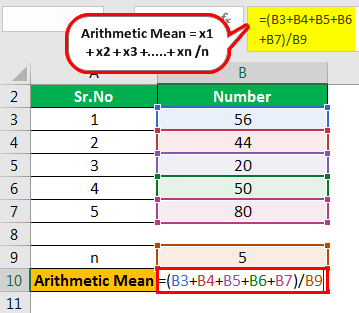
• =56+44+20+50+80/5

Example #2

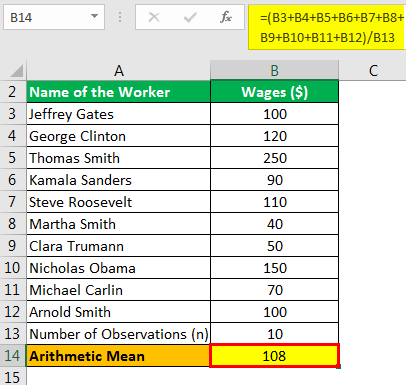
Franklin Inc. is a manufacturing concern with ten workers. There are negotiations between the management of Franklin Inc. and its trade union regarding wages. For this purpose, the CEO of Franklin Inc. wants to calculate the arithmetic mean of salary of workers in the company. The following table gives the wages along with the names of the workers.

Name of the Worker	Wages ($)
Jeffery Gates	100
George Clinton	120
Thomas Smith	250
Kamala Sanders	90
Steve Roosevelt	110
Martha Smith	40
Clara Truman	50
Nicholas Obama	150
Michael Carlin	70
Arnold Smith	100
Number of Observations (n)	10

Calculate the arithmetic mean of wages for the CEO.

Solution

Therefore, the calculation is as follows,

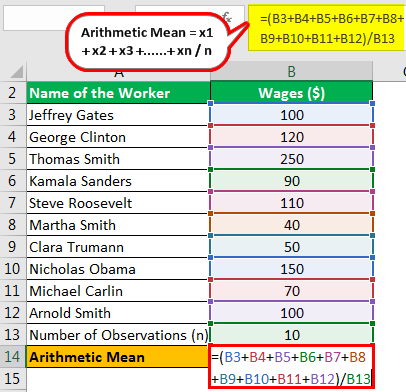
• =(100+120+250+90+110+40+50+150+70+100+10)/10

Example #3

The Principal of a school calls two teachers to his office – one teaches Division A, and the other teaches Division B. Both of them claim that their teaching methods are superior. The Principal decides that the Division, which has a higher arithmetic mean of marks, will have had a better teacher. These are the marks of 7 students each studying in the two Divisions.

Sr. No	Division A	Division B
Student 1	56	70
Student 2	60	65
Student 3	56	60
Student 4	64	65
Student 5	70	75
Student 6	55	55
Student 7	50	65

Find out which Division has higher arithmetic mean.

Solution

Division A

Therefore, the calculation is as follows,

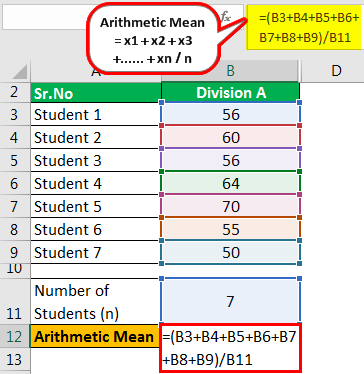
• =(56+60+56+64+70+55+50)/7

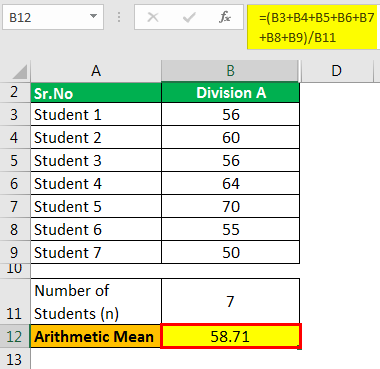
• =58.71 marks

Division B

Therefore, the calculation is as follows,

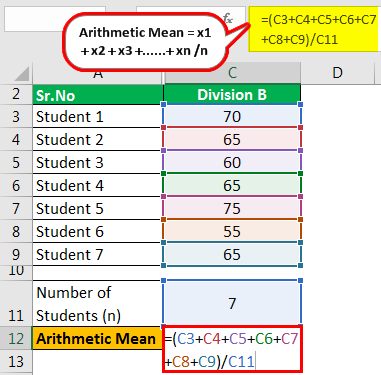
• =(70+65+60+65+75+55+65)/7

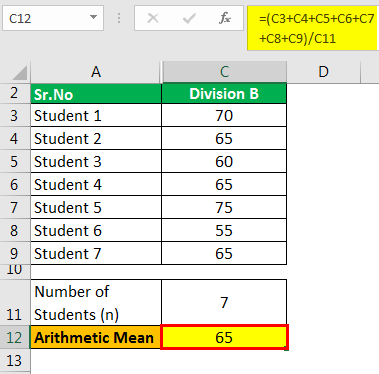
• = 65 marks

The arithmetic mean of Division A is 58.71 marks, and for Division B is 65 marks (higher)

Arithmetic Mean in Excel

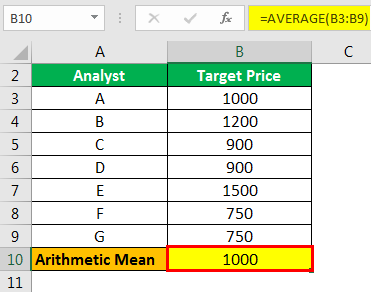
There is company Grandsoft Inc. which is listed on the stock exchanges. Different analysts have given their target price of the stock. Calculate the arithmetic mean of the stock prices.

Analyst	Target Price
A	1000
B	1200
C	900
D	900
E	1500
F	750
G	750

Solution

In Excel, there is an in-built formula to calculate the mean.

Step #1 – Select a blank cell and type =AVERAGE(B2: B8)

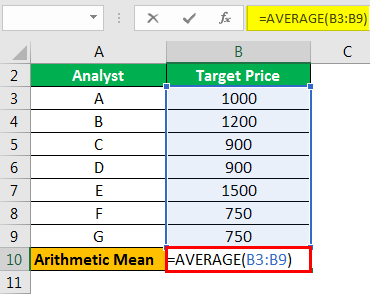
Step #2 – Press Enter to Get the Answer

Relevance and Uses

The arithmetic mean is one of the most important statistics and is most commonly used as the most popular measure of central tendency. It is straightforward to calculate and does not require knowledge of high-end statistics. It is used when all observations in the data set are equally important. If some statements are more important than others, then a weighted mean is used.

Recommended Articles

This has been a guide to Arithmetic Mean Formula. Here we discuss the calculation of arithmetic mean using its formula along with practical examples and a downloadable excel template. You can learn more about excel modeling from the following articles –

• Exponents in Excel
• Formula of Compounding
• Formula of Moving Average
• Weighted Average Excel