Table Of Contents
Frequently Asked Questions (FAQs)
How to find Mode in statistics?
How to find mean median and Mode in statistics?
How to interpret Mode in statistics?
Why is Mode important in statistics?
What Is Mode In Statistics?
The Mode in statistics, for a distribution, refers to a point having such a value where statisticians find the data samples most concentrated. It helps to easily overview the characteristics of any data set in a distribution.
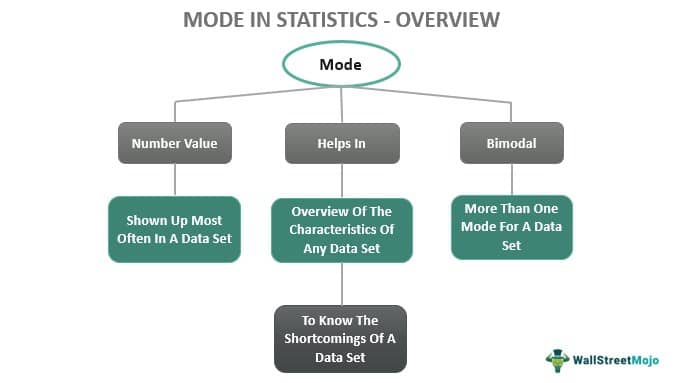
Statisticians, mathematicians, researchers, and analysts do not use Mode for statistics for detailed mathematical analysis of a data set. However, they use it to know the shortcomings of a data set. It can be more than one for a data set, signaling multiple data classes. Since it depends on the frequency of a value in the data set, it cannot make any significant conclusion about the data set.
Key Takeaways
- The Mode in statistics means the value of items in distribution having the highest frequency. Moreover, it can be determined using manual observation.
- It represents the most real data available for interpretation in a distribution of data sets.
- It is best to know the errors in sample collection for a particular type of data set as multiple the most common value can indicate erroneous sample collection.
- A distribution with data sets of different categories can have bi-modal or multi-modal values.
Mode In Statistics Explained
The Mode refers to one of the measures of central tendency in statistics that determine the value with the highest frequency in distribution, whether organized or unorganized, using manual counting. It is called the most common or prevalent value. Croxton and Cowden conceptualized the mean, median, and mode in statistics in 1942 through their book Applied General Statistics, which helped start the branch of statistics.
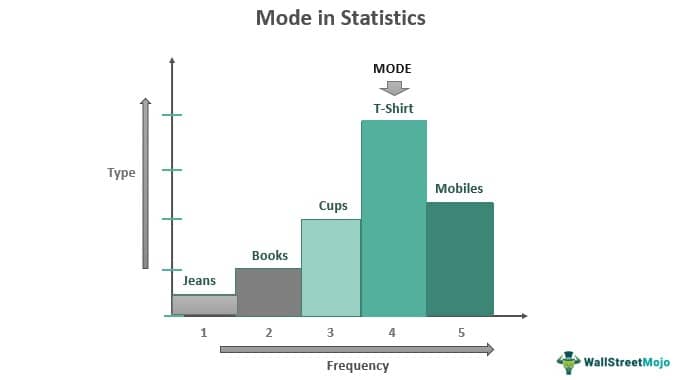
Mode is the easiest way to calculate and understand the nature of a data set. It is valuable as being the best portrayal of data. The extremities of values of data sets in the distribution do not affect its determination. Therefore, the most real value forms an important part of a distribution. One can measure the most common value of a distribution of values of items by plotting the graph of the frequency of the values.
The most common value is not dependent on each value of the data samples. As a result, applying any detailed mathematical calculations and distribution manipulation is impossible. However, any fluctuation or variance in the data sampling greatly impacts its distribution. Moreover, the choices made while grouping data in the data sample can lead to utmost variation in the values of the Mode of the data samples.
In other words, the Mode of a distribution denotes the most used or frequent item.
Formula
Statisticians use the mode formula in statistics to know the highest frequency in a group of data or distribution. They take the most repeated data as the Mode of distribution. It is one of the three important measures related to the central tendency besides mean and median.
Here is the formula that statisticians and analysts use in the calculation of a data set in statistics:
Modeg = L+h (fm-f1)/(fm-f1) + (fm-f2)
Where the modal class = the one with the highest frequency data interval;
- L = lower limit of the said modal class
- h = size of the class interval
- fm = modal class frequency
- f1 = frequency of the class which precedes the modal class; and
- f2 = frequency of the class which succeeds the modal class
Formula To Find The Mode Of Ungrouped Data
For doing so, one has to first arrange the data in ascending or descending manner in terms of their values. After the arranging, one must mark the data values, which are repeated more often. Amongst all the frequent data values, the one having the highest frequency of occurring in the data set is the modal value or the most common value for the set.
Formula To Find The Mode Of Grouped Data
To find the value of grouped data, one has to identify the class interval with the most frequency, known as the modal class. After doing so, one calculates the class size by subtracting the lower limit from the upper limit. Finally, statisticians use the the most common value formula to calculate the Mode for the grouped data after putting all the values in it, as shown below:
Mode = L+h (fm-f1)/(fm-f1) + (fm-f2)
Calculation Example
Here is a mode calculation example to understand the concept and its usage.
| Class Interval | 0−10 | 10−20 | 20−30 | 30−40 | 40−50 |
| Frequency | 8 | 5 | 10 | 4 | 7 |
Modal class = 20-30 as it has the data with the highest frequency
Size of the class interval, h= 10
The lower limit of the above modal class, L= 20
Frequency of the modal class, fm = 10
Frequency of the class which precedes the modal class, f1 = 5; and
Frequency of the class which succeeds the modal class f2 = 4
Therefore, putting all the values in the formula of mode, M =
L+h (fm-f1)/(fm-f1) + (fm-f2)
One can get Mode = 20 +10 (10-5)/ (10-5) + (10-4)
= 20+10*5/11
i.e., (220+50)/11
= 270/11
or, Mode= 24.54 for the above data set.
Example
As discussed below, the best way to understand the basics of this concept is through a mode example.
Let us assume an inventory manager has to know which stock is mostly purchased by the customers and must be replenished accordingly. Therefore, the inventory manager prepares a list of the items in the warehouse with the respective product type and purchase code as below:
| Purchase code | Product Type |
|---|---|
| A | SUNGLASSES |
| B | KIDS GARMENTS |
| C | LAPTOPS |
| D | MOBILE |
| E | SUNGLASSES |
| F | MOBILE |
| G | KIDS GARMENTS |
| H | LAPTOPS |
| I | MOBILE |
| J | SUNGLASSES |
| K | KIDS GARMENTS |
| L | MOBILE |
| M | LAPTOPS |
| N | MOBILE |
| O | KIDS GARMENTS |
For the most common value calculation, one should categorize the above data in the frequency of buying by the customers as below:
| Type | Frequency |
|---|---|
| SUNGLASSES | 3 |
| KIDS GARMENTS | 4 |
| LAPTOPS | 3 |
| MOBILE | 5 |
As a result of the table above, one finds that mobile is bought more frequently than other items in the warehouse inventory. Therefore, mobile is the mode of the data set of our example. Thus, the mode in statistics helps with inventory management.
How To Interpret?
It is the best tool to use along with median and mode of categorical data to know its universal specification. It is also a useful tool for pointing out or learning the errors and problems with the data collection.
As a result, the number of the most common value present in a data signal that the data has samples related to two different populations. Such data where it contains two of them are called bi-modal distribution. Moreover, if it contains more than two in the data set, then the data set is said to have multi-modal distribution.
For instance, a banker wants to know the average time the customers wait to get their work done at the bank. Therefore, he collects customer wait time data using two different services- cash withdrawal and loan application. Hence, after the data is collected, the banker finds two different modes. In other words, the data distribution was bi-modal. So, the bi-modal data suggested to the manager that two separate data sets were collected, which was improper data collection. Hence, the manager should have collected the data for the two services separately for accurate customer-wait results.
