Geometric Mean Return

What is the Geometric Mean Return?

The geometric mean return calculates the average return for the investments which are compounded on the basis of its frequency depending on the time period and it is used to analyze the performance of investment as it indicates the return from an investment.

Geometric Mean Return Formula

You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Geometric Mean Return (wallstreetmojo.com)

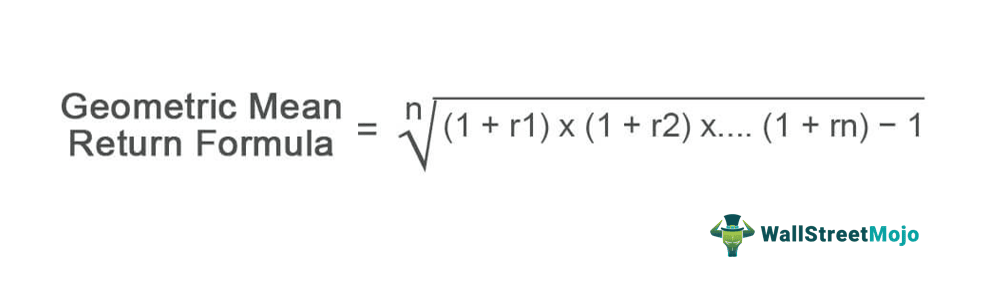
• r = rate of return
• n = number of periods

It is the average set of products technically defined as the ‘n’ ^th root products of the expected number of periods. The focus of the calculation is to present an ‘apple to apple comparison’ when looking at 2 similar kinds of investment options.

Examples

Let us understand the formula with the help of an example:

Assuming the return from $1,000 in a money marketMoney MarketThe money market is a market where institutions and traders trade short-term and open-ended funds. It enables borrowers to readily meet finance requirements through any financial asset that can be readily converted into money, providing an organization with a high level of liquidity and transferability.read more that earns 10% in the first year, 6% in the second year, and 5% in the third year, the Geometric mean return will be:

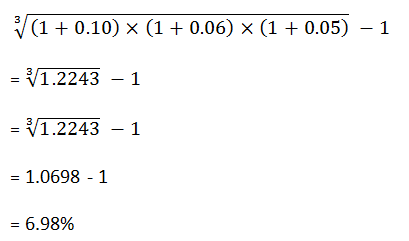
This is the average return taking into consideration the compoundingCompoundingCompounding is a method of investing in which the income generated by an investment is reinvested, and the new principal amount is increased by the amount of income reinvested. Depending on the time period of deposit, interest is added to the principal amount.read more effect. If it had been a Simple average return, it would have taken the summation of the given interest rates and divided it by 3.

Thus to arrive at the value of $1,000 after 3 years, the return will be taken at 6.98% every year.

Year 1

• Interest = $1,000 * 6.98% = $69.80
• Principal = $1,000 + $69.80 = $1,069.80

Year 2

• Interest = $1,069.80 * 6.98% = $74.67
• Principal = $1,069.80 + $74.67 = $1,144.47

Year 3

• Interest = $1,144.47 * 6.98% = $79.88
• Principal = $1,144.47 + $79.88 = $1,224.35
• Thus, the final amount after 3 years will be $1,224.35, which will be equal to compounding the principal amount using the three individual interests compounded on a yearly basis.

Let us consider another instance for comparison:

An investor is holding a stock which has been volatile with returns significantly varying from one year to another. The initial investment was $100 in stock A, and it returned the following:

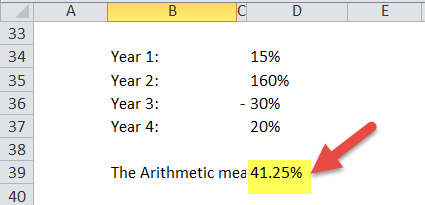
Year 1:  15%

Year 2: 160%

Year 3:  -30%

Year 4: 20%

• The Arithmetic mean will be = [15 + 160 – 30 + 20] / 4 = 165/4 = 41.25%

However, the true return will be:

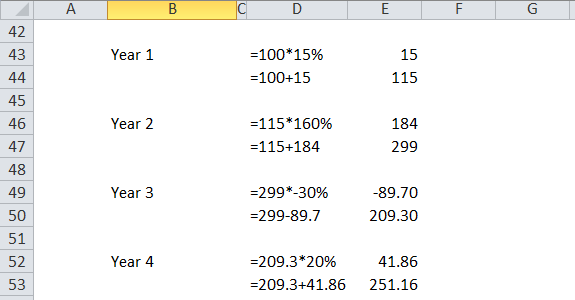
• Year 1 = $100 * 15%   [1.15] = $15 = 100+15 = $115
• Year 2 = $115 * 160%   [2.60] = $184 = 115+184 = $299
• Year 3 = $299 * -30%   [0.70] = $89.70 = 299 – 89.70 = $209.30
• Year 4 = $209.30 * 20% [1.20] = $41.86 = 209.30 + 41.86 = $251.16

The resultant geometric mean, in this case, will be 25.90%. This is much lower than the Arithmetic mean of 41.25%

The issue with Arithmetic mean is that it tends to overstate the actual average return by a significant amount. In the above example, it was observed that in the second xyear the returns had risen by 160% and then fell by 30% which is year over year variance by 190%.

Thus, Arithmetic meanArithmetic MeanArithmetic mean denotes the average of all the observations of a data series. It is the aggregate of all the values in a data set divided by the total count of the observations.read more is easy to use and calculate and can be useful when trying to find the average for various components. However, it is an inappropriate metric to use for determining the actual average return on investment. The geometric mean is highly useful for measuring the performance of a portfolio.

Uses

The uses and benefits of the Geometric Mean Return formula are:

1. This return is specifically used for investments that are compounded. A simple interest account will make use of the Arithmetic average for simplification.
2. It can be used for breaking down the effective rate per holding period return.
3. It is used for Present value and future value cash flow formulas.

Geometric Mean Return Calculator

You can use the following Calculator.

Geometric Mean Return Formula in Excel (with excel template)

Let us now do the same example above in Excel. This is very simple. You need to provide the two inputs of Rate of Numbers and Number of Periods.

You can easily calculate the Geometric Mean in the template provided.

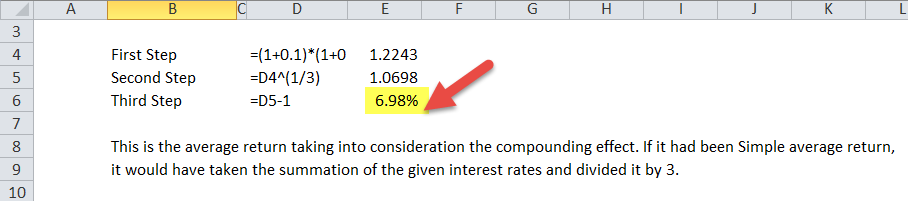
Thus to arrive at the value of $1,000 after 3 years, the return will be taken at 6.98% every year.

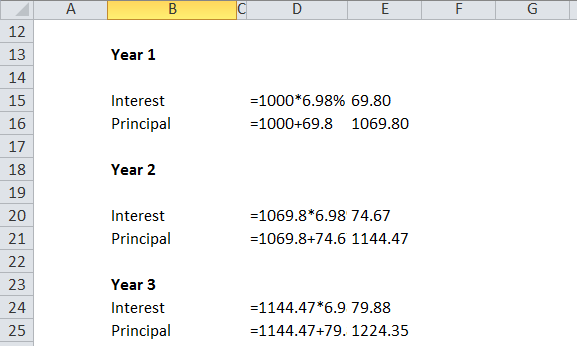
Thus, the final amount after 3 years will be $1,224.35, which will be equal to compounding the principal amount using the 3 individual interests compounded on a yearly basis.

Let us consider another instance for comparison:

However, the true return will be:

The resultant geometric mean, in this case, will be 25.90%. This is much lower than the Arithmetic mean of 41.25%

Recommended Articles

This article has been a guide to Geometric Mean and its definition. Here we discuss the formula of Geometric Mean Return along with examples and excel templates. You may also have a look at these articles below to learn more about Corporate Finance.

• Compare – Geometric Mean vs. Arithmetic Mean
• Harmonic Mean Example
• Population Mean Formula – Examples
• Weighted Mean Formula