CAGR

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

CAGR or compound annual growth rate, refers to the annualized growth rate of investments over a certain duration longer than a year while considering the effect of compounding. This tool helps one gauge and compare the performance of individual assets and portfolios.

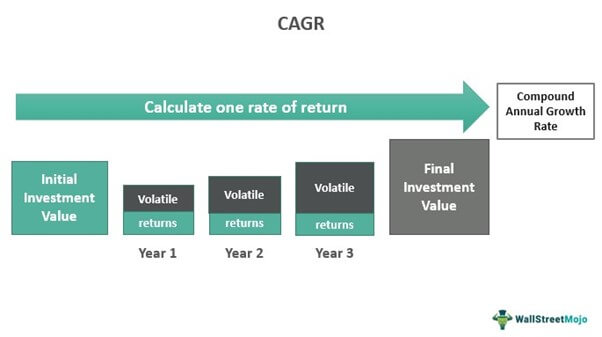
It doesn’t provide individuals with the actual rate of return on investment as it assumes a constant annual growth rate for a particular period. Instead, CAGR smooths out inconsistent growth or volatility. As a result, it makes it easier for one to compare different securities or track the performance of a single one.

Compound Annual Growth Rate (CAGR) Meaning

CAGR refers to a term measuring an investment’s yearly growth over a specific duration taking the effects of compounding into consideration.
For calculating compound annual growth rate, one requires the initial value, final value, and time.
If one finds it difficult to manually compute compound annual growth, using an online CAGR calculator is an ideal solution.
Contrary to the compound annual growth rate, IRR considers inflows, outflows, and timeframes. As a result, it is a much more reliable tool for evaluating complex investments or projects.

Compound Annual Growth Rate Explained

CAGR in finance refers to an investment’s yearly growth rate over a specific period exceeding a year, assuming an individual reinvested the profits during the timeframe. One can utilize this tool to compare investments’ past performance and estimate expected returns. Moreover, individuals and organizations can assess business growth by calculating the compound annual growth rate.

The compound annual growth rate provides the rate at which an investment would have increased if it had grown by the same rate every year. In other words, it does not consider the returns generated each year. Instead, it considers only the initial and final values to compute the average growth rate each year. Thus, it is a representational figure, not the actual return rate. Smoothing out the inconsistent growth diminishes the impact of return volatility.

Calculate CAGR

For calculating compound annual growth rate, one requires an investment’s initial value, final value, and time, i.e., the number of years.

Let us look at the CAGR formula.

CAGR = x 100

Where:

FV is the final value
IV is the initial value
N is the total number of years

One can follow these steps to compute an investment’s compound annual growth rate:

Divide the investment’s initial value by its value at the end of that period.
Raise the quotient to the exponent of 1/N; N is the total number of years,
Subtract 1 from the result.

Lastly, multiply the amount by 100 to convert the result into a percentage.

Example

Let us look at a CAGR example.

Jim invested $1,000 in stock XYZ on April 1, 2015. His portfolio returns are as follows:

From April 1, 2015 to April 1, 2016., his portfolio value surged 50% to $1,500.
On April 1, 2017, the portfolio value was $1750, representing a 16.67% rise.
On April 1, 2018, the portfolio value stood at $1675, dropping 4.78%.
On April 1, 2019, his portfolio value jumped 7.46% to $1800
On April 1, 2020, the value was $2025 after surging 12.5%.

As one can observe, the investment’s growth rate on a year-over-year (YOY) basis is quite inconsistent, owing to price fluctuations in the stock market.

Individuals can compute CAGR over five years using the CAGR formula.

CAGR = x 100 i.e. 6.19%

Individuals who find the manual calculation challenging can use an online CAGR calculator to compute the result without any hassle.

CAGR Advantages

The following are the advantages of compound annual growth rate:

First, it is one of the most accurate ways of computing an investment’s return that goes up or down in value over the holding period.
It helps one to measure the relative performance of the financial assets in their portfolio.
One can use this tool to project expected future returns.

CAGR Limitations

Let us look at a few disadvantages of the compound annual growth rate.

The compound annual growth rate assumes a constant yearly growth rate, whereas in reality, return on investments like stocks, mutual funds, etc., increase and decrease over time.
It doesn’t consider volatility and implies that growth over a certain duration was steady.
It provides individuals with an inflated rate of return as it ignores the cash inflows and outflows during the investment duration.

CAGR vs IRR

Internal rate of return or IRR refers to the discount rate that makes the net present value (NPV) of a project’s positive and negative cash flows nil. It projects the profitability of potential investments.

Unlike the compound annual growth rate, it considers multiple periods and cash flows. As a result, It is much more flexible. Moreover, experts consider it a more suitable tool for assessing complicated investments or projects.

Frequently Asked Questions (FAQs)

1. How to use CAGR to forecast?

To find the future values using the compound annual growth of any data series, one has to multiply the last datum of that series by (1+CAGR) as many times as necessary.

2. Can CAGR be calculated for months?

As the name suggests, it measures investments’ annual annualized growth rate over time. One can use the compound monthly growth rate (CMGR) formula to compute an investment’s average month-over-month growth. It is similar to the compound annual growth rate formula.

3. Does CAGR include inflation?

No, the compound annual growth rate does not consider inflation.

4. What is a good CAGR for a portfolio?

There is no right answer to this question. It depends on various factors, such as an individual’s financial goals, risk appetite, and investment time horizon. For example, if one is looking to earn stable returns by building a balanced portfolio comprising debt and equity, a compound annual growth rate of 8% to 12% can be considered decent. However, the same range will not be as attractive for aggressive investors with a 100% equity portfolio.