Relative Change

Last Updated :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What is Relative Change?

Relative change shows the change of a value of an indicator in the first period and in percentage terms, i.e., Relative change is calculated by subtracting the value of the indicator in the first period from the value of the indicator in the second period which is then divided by the value of the indicator in the first period and the result is taken out in percentage terms.

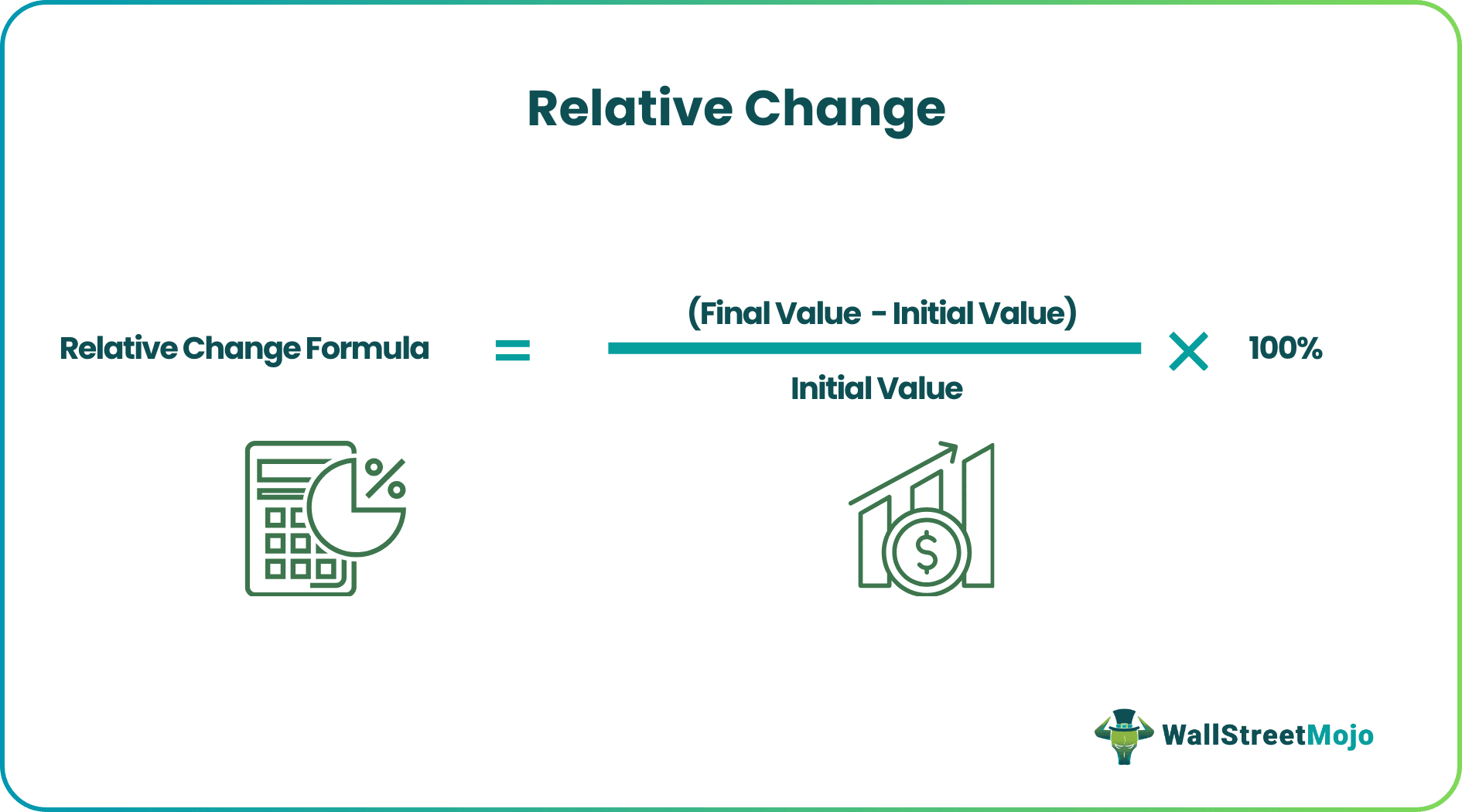
The formula for relative change is very simple, and it is derived by initially deducting the initial value of the variable from the final value, then dividing the result by the initial value, and then finally multiplying by 100% to express in terms of percentage. Mathematically, it is represented as,

Relative Change = (Final value – Initial value) / Initial value * 100%

What is Relative Change?

Relative change, also referred to as percentage change or percent change, is a metric used to measure the proportional difference between two values or quantities. It quantifies the change relative to the original or reference value.
The formula for calculating relative change is Relative Change = (New Value - Old Value) / Old Value * 100%. This formula expresses the change as a percentage of the original value.
Relative change finds widespread application in various contexts, including financial performance analysis, tracking economic indicators, monitoring population growth rates, and evaluating scientific experiments.

Calculation of the Relative Change (Step by Step)

The formula for relative change can be derived by using the following steps:

Firstly, determine the initial value of the variable. For instance, the revenue earned by a company in the previous year can be an example of an initial value of the revenue.
Next, determine the final value of the variable. In the above example, the revenue earned in the following year can be regarded as the final value of the revenue.
Next, deduct the initial value from the final value to derive the absolute change in the variable. In the example, the increase in revenue in the following year.

Absolute change = Final value – Initial value

Relative change Formula = (Final value – Initial value) / Initial value * 100%

Examples

Example #1

Let us take the example of a small business owner who wants to compare the current year’s revenue with the revenue generated in the previous year. In the current year, the business managed revenue of $53,250, while the revenue clocked last year was $51,000. Calculate the relative change in the revenue in the current year.

Therefore, the % change in the revenue of the current year can be calculated using the above formula as,

% Change = ($53,250 – $51,000) / $51,000 * 100%

% Change= 4.41%

Therefore, the current year revenue grew by 4.41% as compared to the revenue generated last year.

Example #2

Let us take the example of an apartment that was valued at $1,200,000 last month. Calculate the relative change in the valuation of the house if the valuation today has moved to $1,150,000.

Therefore, the % change in the valuation today can be calculated using the above formula as,

% change = ($1,150,000 – $1,200,000) / $1,200,000 * 100%

% Change = -4.17%

Therefore, the valuation of the apartment today is 4.17% lower as compared to the last month’s valuation.

Example #3

Let us take the example where a business owner has started a new product line. Now, because of the new product, the revenue has increased from $78,000 to $89,000, and the cost of sales has increased from $56,000 to $66,000. Determine whether the value addition for the business owner in terms of absolute change and relative change.

Absolute Change in Revenue

Absolute Change in Revenue = $89,000 - $78,000
= $11,000

Absolute Change in the Cost of Sales

Absolute change in the cost of sales = $66,000 - $56,000
= $10,000

Incremental Benefit in Absolute Terms

Incremental benefit in absolute terms = Absolute change in revenue - Absolute change in cost of sales
= $11,000 - $10,000
= $1,000

% Change in Revenue

% change in revenue = ($89,000 - $78,000) / $78,000 * 100%
= 14.10%

% Change in Cost of Sales

% change in cost of sales = ($66,000 - $56,000) / $56,000 * 100%
= 17.86%

Incremental Benefit in Relative Terms

Incremental benefit in relative terms = % change in revenue - % change in the cost of sales
= 14.10% - 17.86%
= -3.76%

Therefore, the business is making benefit in absolute terms ($1,000) but is losing in relative terms (-3.76%) because the relative change in the cost of sales is higher than that of revenue due to its lower base.

Relative Change Calculator

You can use this Relative Change Calculator.

Relevance and Uses

The concept of relative change is important because, at times, it is impossible to compare the absolute changes in the value of two entities because of the scale or size, i.e., a small change in a large value can be greater than a significantly large change in a small value. For instance, 10% in 5000 is equal to 500 is higher than 75% of 200, which is equal to 150, although, in terms of % change, it is the other way round.

In such a scenario, the percentage change is very handy as it takes the problem of scale-out of the equation as it is a unitless value expressed either as a fraction or percentage. The relative change formula has applications in every field, such as financial metrics, scientific values, historical values, etc.

Frequently Asked Questions (FAQs)

1. What does a positive or negative relative change indicate?

A positive relative change indicates an increase or growth in the measured quantity compared to the reference value. It suggests that the quantity has expanded by a certain percentage or proportion. Conversely, a negative relative change indicates a decrease or decline in the measured quantity relative to the reference value, signifying a contraction or reduction in percentage terms.

2. What are the limitations associated with the application of the relative change technique?

The application of the relative change technique has certain limitations. One limitation is that it does not provide information about the absolute values or magnitudes of the compared quantities. Additionally, the relative change can be influenced by the choice of the reference value, making it important to select an appropriate baseline carefully.

3. How can relative change be used in financial analysis?

Relative change can be used in financial analysis to assess the performance of various financial metrics or indicators over time. By comparing the values of financial variables, such as revenues, profits, or returns, relative change provides insights into the percentage change in these measures. It allows analysts to evaluate the growth or decline of financial figures and assess the relative performance of different companies or investment opportunities.