LOG Excel Function

The LOG function in Excel is used to calculate the logarithm of a given number. Still, the catch is that the user’s base for the number is to be provided. It is a built-in function that we can access from Excel’s “Formulas” tab. It takes two arguments: one is for the number, and another is for the base.

LOG In Excel

The LOG function in Excel computes the logarithm of a number to the base that we specify. It is categorized as a Math/Trigonometry function in Excel. Therefore, the LOG function in Excel always returns a numeric value.

In mathematics, the logarithm is the opposite of the exponentiation. It means the logarithmic value of any given number is the exponent to which we must raise the base to produce that number. For example,

2⁵= 32

For a given number 32, 5 is the exponent to which base 2 has been raised to produce the number 32. So, a LOG of 32 will be 5.

Mathematically, we write it as log232 =5. A LOG of 32 to the base 2 is 5.

LOG Formula in Excel

Number: It is a positive real number (should not be a 0) for which we want to calculate the logarithm in Excel.

Base: It is an optional argument, it is the base on which the logarithmic value is calculated, and the LOG function in Excel, by default, takes the base as 10.

How to Use the LOG Function in Excel?

The LOG function in Excel is very simple and easy to use. Let us understand the working of the LOG function in Excel by some LOG formula examples.

You can download this LOG Function Excel Template here – LOG Function Excel Template

The logarithmic function is used for mathematical operations and is widely used in financial statisticsWidely Used In Financial Statistics Statistics is the science behind identifying, collecting, organizing and summarizing, analyzing, interpreting, and finally, presenting such data, either qualitative or quantitative, which helps make better and effective decisions with relevance.read more. In business analytics, LOG in Excel is often used with other tools for regression analysisRegression Analysis Regression analysis depicts how dependent variables will change when one or more independent variables change due to factors, and it is used to analyze the relationship between dependent and independent variables. Y = a + bX + E is the formula.read more and plotting graphs for data representation. For example, logarithmic functions are used for graphical representation when the data rate of changeRate Of Change Rate of change (ROC) defines the percentage change of a variable like securities over a certain time with respect to its original value. read more in the data increases or decreases quickly.

The POWER function returns the result of a number raised to a power. So, inversely, the LOG function in Excel returns the power (exponent) to which the base is raised.

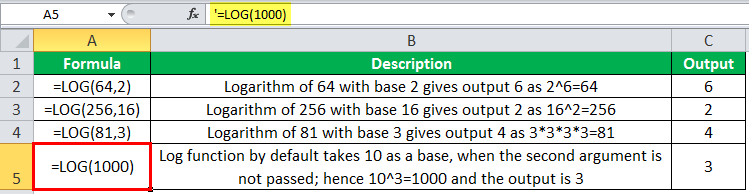
LOG in Excel Example #1

For example, 4^{5 =}1024, using the POWER functionPOWER Function POWER function calculates the power of a given number or base. To use this function you can use the keyword =POWER( in a cell and provide two arguments one as number and another as power.read more, we would write it as POWER(4,5) = 1024. If we nest this formula of the POWER function inside the LOG function in Excel, providing the base as 4, we will get the exponent, which is passed as a second argument in the POWER function.

The output of the POWER function is passed as the first argument to the LOG function in Excel, and it further computes the result.

We can use the LOG function in Excel in many ways. First, the logarithm helps to solve real-world problems. For example, the magnitude of an Earthquake is calculated as the logarithm of the amplitude of the seismic waves generated.

A LOG formula represents the magnitude of an earthquake:

R=log₁₀(A/A₀)

When A is the measurement of the amplitude of an earthquake wave, and A0 is the smallest amplitude recorded of seismic activity. If we have the values of A and A0, we can easily calculate the magnitude of the earthquake in Excel by the LOG formula:

=LOG((A/A₀),10)

LOG in Excel Example #2

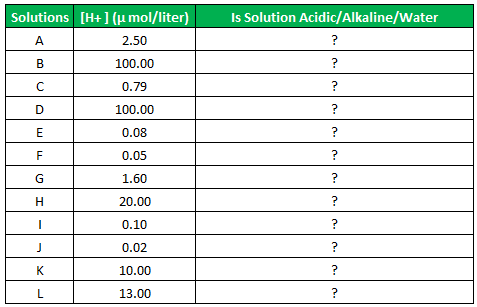
Suppose we have samples of solutions labeled with alphabets A, B, C….L. We are provided with the [H+] ion concentration in µ mol/liter in the Excel sheet in column B. We want to find which solution is acidic, alkaline, or water. The data table is given below:

The acidic and the basic nature of a chemical solution are measured by its pH value, which is calculated by the formula:

pH=-log₁₀[H+]

If pH is less than 7, it is an acidic solution; if a pH is greater than 7, it is a basic(alkaline) solution, and when pH is 7, it is neutral, which is neither acidic nor basic like water.

So, to find the acidic and basic nature of the solution, we will use the LOG in Excel and check if the logarithmic value is less than, greater than, or equal to 7.

Since the given hydrogen concentration is in a unit of µmol/liter, the value will be X*10^-6

So, the LOG in Excel to find the nature of the solution.

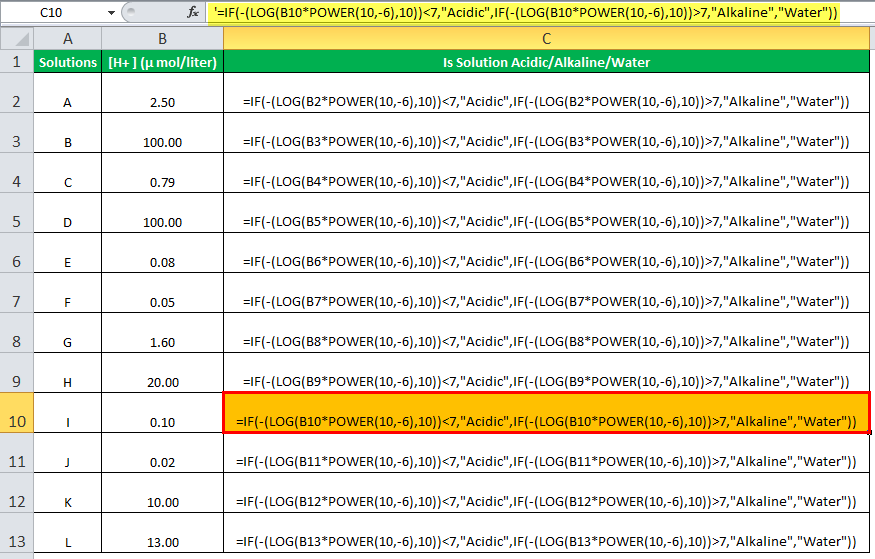
=IF(-(LOG(B4*POWER(10,-6),10))<7,”Acidic”,IF(-(LOG(B4*POWER(10,-6),10))>7,”Alkaline”,”Water”))+

Computing the value of Log of [H⁺] concentration * Power(10,-6) since the unit used is µmol/liter and checking, using the IF function if the value is greater than, less than, or equal to 7.

Using the formula in other cells, we have,

Output:

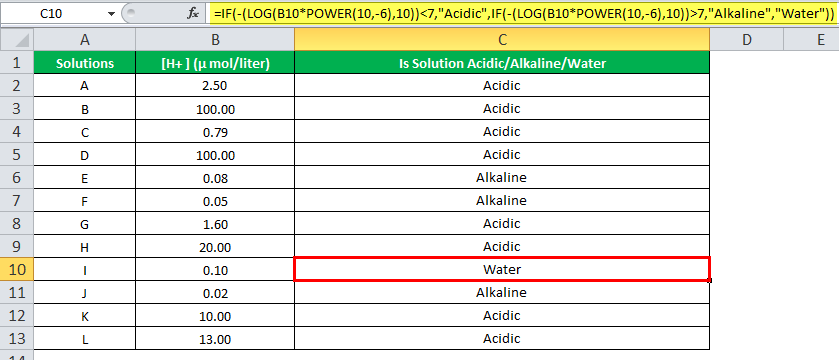
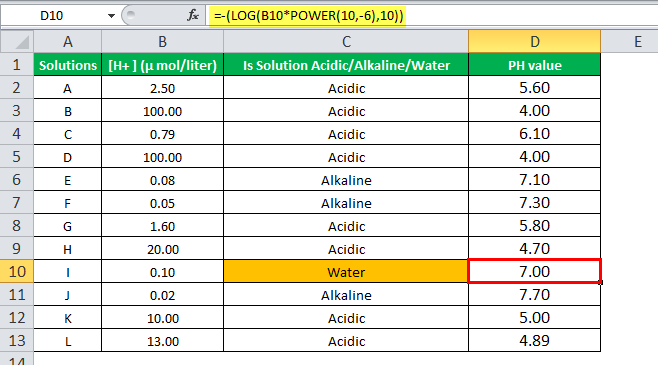
The solution labeled with I has a pH value equal to 7. Hence, it is pure water.

LOG in Excel Example #3

In computer science, every algorithm has its efficiency measured in how fast it fetches the result or gives an output. This efficiency is calculated technically by the time complexity. Time complexity describes the amount of time an algorithm will take to execute.

There are different algorithms for searching an item in an array list, e.g., bubble sort, quick sort, merge sort, binary sort, etc. Moreover, every algorithm has different efficiency in terms of its time complexity.

To understand, consider an example.

We have a sorted array,

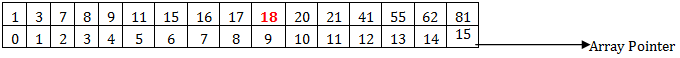
We want to search for the number 18 from the data array.

This algorithm follows the divide and rule methodology, where it divides the set equally at each step of iteration and searches for the item. When it finds the item, the loops (iteration) get terminated and return the value.

Step 1:

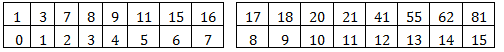
Step 2:

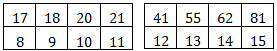
Step 3:

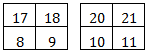
Step 4:

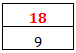
We found number 18 at position 9, and it took four steps to search the item using the binary search algorithm.

So, the complexity of the binary search is calculated as:

log₂N, where n is the number of items.

=LOG(16,2) = 4

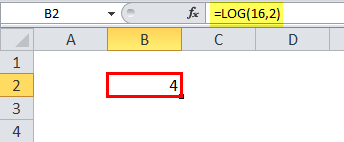
Hence, to search for an item in an array of items, the binary search will take log2N steps.

Suppose we are provided with a list that contains the total number of items, and to search for an item from these items, we are using the Binary search algorithm. First, we have to find how many steps it will take to find an item from the given items.

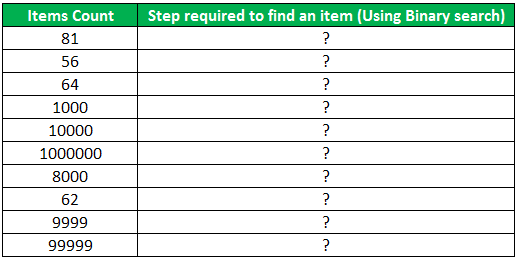
Again, we will use the LOG in Excel to calculate the complexity.

The LOG formula will be: = ROUND(LOG(A6,2),0)

The result could be in decimal, so we have rounded the result of 0 places of digits.

Concatenating with the “String Steps Required is,” we have:

=”Steps Required are”&” “&ROUND(LOG(A6,2),0)

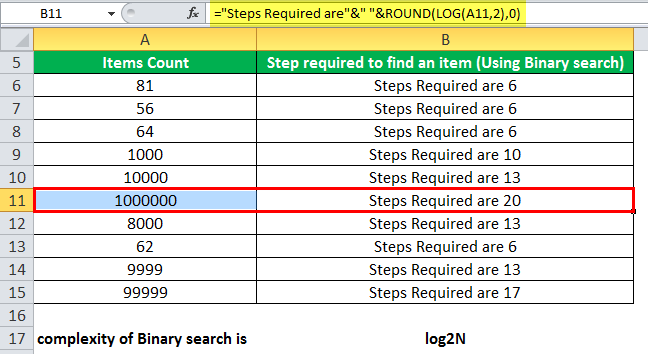
For searching for an item from an array of 1000000 items, the binary search will take only 20 steps only.

The LOG functions are also widely used in economics for stock price indexing graphs. These graphs are very useful for checking the prices going down or up.

LOG Excel Function